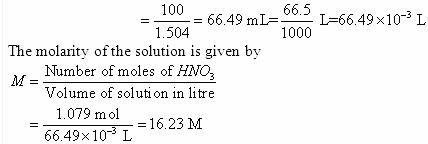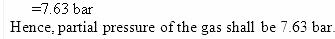Please Visit our new Website here
Learn more at http://skmclasses.weebly.com/iit-jee-home-tuitions-bangalore.html
search for videos in http://skmclasses.weebly.com
Twitter – https://twitter.com/ZookeeperPhy
Facebook – https://www.facebook.com/IIT.JEE.by.Prof.Subhashish/
Blog – http://skmclasses.kinja.com
Free Pdf e-Book download for IIT-JEE, CBSE, ISc, CET Physics Chemistry Maths from Professor Subhashish SKMClasses can be done at
Download the following FREE pdf e-Books ( Chapter wise / Topic wise solutions, Written by Prof. Subhashish Chattopadhyay SKMClasses Bangalore )
IIT-JEE, NCERT / CBSE, I.Sc., PU, Board exam, EAMCET, BITS Chemistry Books with lots of Examples ( Free pdf download of Chemistry Books, Chapter wise / Topic wise Questions and Solutions )
8 ] CBSE 12 & IIT-JEE Chemistry Survival Guide-Stoichiometry Titration by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Stoichiometry Titration ” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Chemistry Survival Guide-Stoichiometry Titration by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Chemistry, CET, VIT, Manipal, SRM and other exams.
This e-Book covers several examples of Stoichiometry Titrations, Heating effects in several salts, colours or colors of the precipitates, Empirical formulae calculation, Limiting reagents, Titration examples, Equivalent weight, milli-equivalent weight, What mass or moles is reacting with how much ? How much is oxidised ? How much is Reduced ? Several Complicated examples and many more, and various incomplete dictionary kinds of collection for Course of IIT-JEE, CET, etc with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions.
CBSE 12 & IIT-JEE Chem Survival Guide-Stoichiometry Titration by Prof. Subhashish
:-{D
7 ] CBSE 12 & IIT-JEE Chemistry Survival Guide-Redox Reactions by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Redox Reactions ” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Chemistry Survival Guide-Redox Reactions by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Chemistry, CET, VIT, Manipal, SRM and other exams.
This e-Book covers more than 60 examples of Redox Reactions, Several Complicated examples and many more, and various incomplete dictionary kinds of collection for Course of IIT-JEE, CET, etc with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions.
CBSE 12 & IIT-JEE Chem Survival Guide-Redox Reactions by Prof. Subhashish
:-{D
6 ] CBSE 12 & IIT-JEE Chemistry Survival Guide-Electrochemistry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Electrochemistry ” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Chemistry Survival Guide-Electrochemistry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Chemistry, CET, VIT, Manipal, SRM and other exams.
This e-Book covers Electrochemistry, Oxidation Potentail, Reduction Potential, Electrode Potential, Reactivity Series, Battery, Nernst Equation, Variation of Voltage with concentration, Electrolyte, Electrolysis, Salt Bridge, Daniel Cell, Primary Cell, Secondary Cell, Galvanic Cell, Electrolytic Cell, Conductivity, Kohlrausch’s Law and many more, and various incomplete dictionary kinds of collection for Course of IIT-JEE, CET, etc with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions.
CBSE 12 & IIT-JEE Chem Survival Guide-ElectroChemistry by Prof. Subhashish
:-{D
5 ] CBSE 12 & IIT-JEE Organic Chemistry Survival Guide-Reduction Methods by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Reduction Methods ” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Organic Chemistry Survival Guide-Reduction Methods by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II AP-Chemistry IGCSE IB AP-Chemistry, CET, VIT, Manipal, SRM and other exams.
This e-Book covers Various kinds of Reduction Methods in Organic Chemistry. Covers Gilmann’s Reagent, Grignard Reagent, Trimethyl Silyl Iodide, Silyl Wittig Reaction, Hydrogen with Ni, Zn, Pd Palladium, Bakers Yeast, Wolf Kishner, Wilkinson’s Catalyst, Birch Reduction, Lindlar’s Catalyst, Benkeser Reduction, Reduction with HCO2H, Sodium Boro Hydride NaBH4, Veils Meier Reaction, Luche’s Reagent, Super Hydride, Sodium Cyno boro hydride, Dibal H, Adams Catalyst, Rosen Mund Reduction, Various Lithium Aluminium Hydrides, NaNH2, and many more, and various incomplete dictionary kinds of collection for Course of IIT-JEE, CET, etc with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions.
CBSE 12 & IIT-JEE Organic Chem Survival Guide-Reduction methods by Prof. Subhashish
:-{D
4 ] CBSE 12 & IIT-JEE Organic Chemistry Survival Guide-Oxidation Methods by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Oxidation Methods ” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Organic Chemistry Survival Guide-Oxidation Methods by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Chemistry, CET, VIT, Manipal, SRM and other exams.
This e-Book covers Various kinds of Oxidation Methods in Organic Chemistry. Covers Sarett’s Reagent, PCC, Chromium Oxide, Osmium Oxide, Manganese Oxide, Silver oxides, Ruthenuim Oxide, Hydrogen Peroxide, Selenium dioxide, KMnO4, Jones, Julia Colonna, DCC, Corey’s, Moffats, Ley Oxidation, MPV, Fetizon, Frmy’s Salt, Elbs Persulphate Oxidation, Sodiumperiodate, Palladium Chloride, Copper Chloride, Sharpless epoxidation, and many more, and various incomplete dictionary kinds of collection for Course of IIT-JEE, CET, etc with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions.Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions.
CBSE 12 & IIT-JEE Organic Chem Survival Guide-Oxidation methods by Prof. Subhashish
IIT-JEE, NCERT / CBSE, I.Sc., PU, Board exam, EAMCET, BITS Math Books with lots of Questions and Solutions, Examples ( Free pdf download of Math Books, Chapter wise / Topic wise Solutions )
15 ] CBSE & IIT-JEE Math Survival Guide-Hyperbola Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Hyperbola Coordinate Geometry” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Hyperbola Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Hyperbola Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Hyperbola Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE & IIT-JEE Math Survival Guide-Hyperbola by Prof. Subhashish
:-{D
14 ] CBSE & IIT-JEE Math Survival Guide-Ellipse Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Ellipse Coordinate Geometry” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Ellipse Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Ellipse Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Ellipse Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE & IIT-JEE Math Survival Guide-Ellipse by Prof. Subhashish
:-{D
13 ] CBSE & IIT-JEE Math Survival Guide-Parabola Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Parabola Coordinate Geometry” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Parabola Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Parabola Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Parabola Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE & IIT-JEE Math Survival Guide-Parabola by Prof. Subhashish
:-{D
12 ] CBSE & IIT-JEE Math Survival Guide-Pair of Straight Lines Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Pair of Straight Lines Coordinate Geometry” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Pair of Straight Lines Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Pair of Straight Lines Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Pair of Straight Lines Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE & IIT-JEE Math Survival Guide-Pair of Straight Lines by Prof. Subhashish
:-{D
11 ] CBSE 11 & IIT-JEE Math Survival Guide-Circles Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Circles Coordinate Geometry” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Circles Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Circles Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Circles Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 11 & IIT-JEE Math Survival Guide-Circles by Prof. Subhashish
:-{D
10 ] CBSE 11 & IIT-JEE Math Survival Guide-Straight Lines Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Lines Coordinate Geometry” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Lines Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Straight Lines Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Straight Lines Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 11 & IIT-JEE Math Survival Guide-Straight Lines by Prof. Subhashish
:-{D
9 ] CBSE 11 & IIT-JEE Math Survival Guide-Complex Numbers or Imaginary Numbers by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Complex Numbers or Imaginary Numbers” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Complex Numbers or Imaginary Numbers by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Complex Numbers or Imaginary Numbers with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Complex Numbers or Imaginary Numbers, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 11 & IIT-JEE Math Survival Guide-Complex Number by Prof. Subhashish
:-{D
8 ] CBSE 12 & IIT-JEE Math Survival Guide-Quadratic Equations by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Quadratic Equations” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Quadratic Equation by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Quadratic Equations with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Quadratic Equations, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 11 & IIT-JEE Math Survival Guide-Quadratic Equation by Prof. Subhashish
:-{D
7 ] CBSE 12 & IIT-JEE Math Survival Guide-Continuity and Differentiability by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Continuity & Differentiability” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Continuity and Differentiability by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Continuity and Differentiability with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Continuity and Differentiability, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 12 & IIT-JEE Math Survival Guide-Continuity & Differentiability by Prof. Subhashish
:-{D
6 ] CBSE 12 & IIT-JEE Math Survival Guide-Relations and Functions by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Relations & Functions” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Relations and Functions by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Relations and Functions with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Relations and Functions, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 12 & IIT-JEE Math Survival Guide-Relations & Functions by Prof. Subhashish
:-{D
5 ] CBSE 12 & IIT-JEE Math Survival Guide-Graphs and Functions by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Graphs & Functions” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Graphs and Functions by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Graphs and Functions with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Graphs and Functions, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 12 & IIT-JEE Math Survival Guide-Functions & Graphs by Prof. Subhashish
:-{D
4 ] CBSE 12 & IIT-JEE Math Survival Guide-Indefinite Integrals by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Indefinite Integrals & Calculus” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Indefinite Integrals by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II CET CEE IGCSE IB AP-Mathematics and other exams.
This e-Book covers Indefinite Integrals with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Indefinite Integrals, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CBSE 12 & IIT-JEE Math Survival Guide-Indefinite Integrals by Prof. Subhashish
:-{D
3 ] CBSE 12 & IIT-JEE Math Survival Guide-Area & Volume by Prof. Subhashish
Description – “Spoon Feeding Area and Volume ” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 and IIT-JEE Math Survival Guide-Area and Volume by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Mathematics and other exams.
This e-Book covers various kinds of graphs, such as graph of Ln x, ( ln x )/x, x Ln x, floor x [ x ] , Shifting of graphs, roots of Quadratic, cubic, and other higher powers of x ( polynomials ), asymptotes, ( How to find Asymptotes ) etc. Volume by revolution and hundreds of Area problems of IIT-JEE, AIEEE, CET, etc with CBSE, AIEEE, IIT-JEE ( Main and Advanced ) Problems and Solutions.
CBSE 12 & IIT-JEE Math Survival Guide-Area & Volume by Prof. Subhashish
:-{D
2 ] CBSE 12 & IIT-JEE Math Survival Guide-Definite Integrals by Prof. Subhashish
Description – “Spoon Feeding Definite Integrals ” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Definite Integrals by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Mathematics and other exams.
CBSE 12 & IIT-JEE Math Survival Guide-Definite Integrals by Prof. Subhashish
This e-Book covers Definite Integrals with [ x ] greatest integer functions, { x } fraction function, Max and Min functions. Gamma function, Beta function, Integration after converting to Complex number, Leibnitz forms of Differentiating Integrals, L Hospital’s rule applied to limits with Integrals, Inequalities of Integrals, Rules / Tricks / Properties of Definite Integrals, with CBSE, COMEDK, IIT-JEE ( Main and Advanced ) Problems and Solutions.
:-{D
1 ] CBSE 12 Math Survival Guide-Differential Equations by Prof. Subhashish.pdf
Description – “Spoon Feeding Differential Equations ” for IIT-JEE, I.Sc. , CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Differential Equations by Prof. Subhashish Chattopadhyay SKMClasses Bangalore Useful for I.Sc. PU-II COMEDK IGCSE IB AP-Mathematics and other exams.
CBSE 12 & IIT-JEE Math Survival Guide-Differential Equations by Prof. Subhashish
This e-Book covers all kinds of Differential equations, and methods to solve them. There is a priority checklist for the approach to be taken for solving the problems. Covers ISc, CBSE, COMEDK, IIT-JEE problems, Linear, Homogeneous, Variable separable by substitution, Exact, Reducible to exact, Bernoulli, Integrating Factors or Multiplying Factors, even Clairaut’s Differential Equations ( IIT-JEE 1999, Bihar CEE 1999 )
–
Various States have different names for the Engineering Entrance Exams.
CET – Common Engineering Entrance Test or Common Entrance Test is for Karnataka, Maharastra, Gujrat, Himachal Pradesh, J&K
GUJCET Exam – Gujarat Entrance Common Entrance Test – Engineering
HPCET – Himachal Pradesh Common Entrance Test
CEE – Commissionerate of Entrance Examinations Kerala. Some people say Common Entrance Exam. The exam in Kerala actually is known as KEAM – Kerala
Engineering Agriculture Medical Degree.
ASSAM CEE – Assam Combined Entrance Exam
EAMCET – Engineering and Medical Common Entrance Test
MP PET – Madhya Pradesh Pre Engineering Test. Randomly I liked lots of Physics Questions of MP-PET, as these were of very high quality / interesting.
RPET or R-PET – Rajasthan Pre Engineering Test
WBJEE or WB-JEE – West Bengal Joint Entrance Exam. The questions of these are very good / high quality.
UPSEE – Utter Pradesh State Entrance Exam
BCECEB – Bihar Combined Entrance Competitive Examination Board. The exam name is BCECE. Some call it as Bihar Combined Engineering Entrance Exam BCEEE or
BCECE (Bihar Combined Entrance Competitive Examination)
OJEE – Orissa Joint Entrance Exam
Tamilnadu does not have any state ( common ) entrance test. The admissions in colleges / universities are through standard 12 marks.
TNEA is a State Engineering Entrance Examination, which is conducted by Anna University. Tamil Nadu Engineering Admission.
COMEDK PGET – Consortium of Medical, Engineering and Dental Colleges of Karnataka for PG Post Graduate
NATA – National Aptitude Test in Architecture. National Institute of Advanced Studies in Architecture (NIASA) conducts this.
ISAT by IISAT – Indian Institute of Space Science and Technology (IISAT) Admission Test (ISAT) is a National Level Entrance Examination.
NAT – National Aptitude Test by Society for Research & Development in Education (SRDE), New Delhi
ENAT – EPSI National Admission Test. by Manipal Institute of Technology. Manipal Online Entrance Test Manipal-OET
VITEEE – VIT Engineering Entrance Exam, Vellore Institute of Technology. Conducted by VIT university
BITSAT – Birla Institute of Technology and Science Admission Test.
Punjab PET – Punjab Engineering Admission, Pre Engineering Test
ASSAM CEE – Assam Combined Entrance Exam
Tripura JEE – Tripura Joint Entrance Exam
NEE – NERIST Entrance Examination. Conducted by the North Eastern Regional Institute of Science & Technology (NERIST), Nirjuli, Itanagar, Arunachal Pradesh
1 ] CET CEE EAMCET JEE Math Survival Guide-Hyperbola Coordinate Geometry by Prof. Subhashish Chattopadhyay
Description – “Spoon Feeding Hyperbola Coordinate Geometry” for IIT-JEE, I.Sc., CBSE, Karnataka PU, State Boards etc. CBSE Standard 12 Math Survival Guide-Hyperbola Coordinate Geometry by Prof. Subhashish Chattopadhyay SKMClasses Bangalore. Useful for I.Sc. PU-II CET CEE COMED-K IGCSE IB AP-Mathematics and other exams.
This e-Book covers Hyperbola Coordinate Geometry with lots of Video explanations. The classroom teaching videos can be seen by clicking on the given links. The videos can be downloaded also. Hundreds of tricky problems solved. Rules / Tricks / Properties of Hyperbola Coordinate Geometry, with CBSE, COMED-K, IIT-JEE ( Main and Advanced ) Problems and Solutions. Includes NCERT / CBSE Text Book Solutions, Chapter wise Solutions, AIEEE ( Now known as IIT-JEE main ) Solutions, Roorkey Entrance Exam Solutions, CET, CEE, PET, EAMCET Solutions. R D Sharma Solutions, R S Aggarwal’s Solutions.
CET CEE PET EAMCET JEE Math Survival Guide-Hyperbola by Prof. Subhashish
:-{D
https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/

Many more free pdf e-Books are available at ( such as H C Verma Concepts of Physics Solutions, Arihant Books, free download eBooks for IIT JEE guides, AIEEE IIT JEE advanced Chapter wise solutions, preparation materials )
1 ] A Guide Book to Mechanism in Organic Chemistry by Peter Sykes
A_GUIDE_BOOK_TO_MECHANISM_IN_ORGANIC_CHEMISTRY
2 ] Nomenclature of Inorganic Chemistry – IUPAC Recommendations 2005
Nomenclature of Inorganic Chemistry – IUPAC Recommendations 2005
3 ] Linear Algebra For Dummies
4 ] Calculus Workbook For Dummies
5 ] Differential Equations For Dummies
Differential_Equations_For_Dummies
6 ] Linear Algebra by Jim Hefferon
7 ] Mathematics – Puzzles from around the world
Mathematics—Puzzles-from-around-the-world
8 ] Graph Theory by Reinhard Diestel
9 ] Electronics for Dummies
10 ] Electronics Projects for Dummies
Electronics Projects For Dummies
11 ] Physics For Dummies
12 ] Physics Workbook For Dummies
13 ] Inorganic Chemistry James E. House
Inorganic Chemistry James E. House
14 ] Inorganic Chemistry by Cox
15 ] Inorganic Chemistry 5th Edition Miessler
Inorganic Chemistry 5th Edition Miessler
16 ] Fundamentals of Organic Chemistry Solomon
Fundamentals of Organic Chemistry Solomon
17 ] Illustrated Guide to Home Chemistry Experiments
Illustrated Guide to Home Chemistry Experiments
:-{D
e-Book-e-Book-e-Book-e-Book-e-Book-e-Book-e-Book-e-Book-e-Book-e-Book–e-Book
If you want to sell your House, why do you have to pay 2% to a Broker or to a website ?
You can advertise for free to sell your House at free4u.info
Professor Subhashish Chattopadhyay is providing a Social Service for all in Bangalore, to advertise for Free
If you want to sell your Car, why do you have to pay 2% to a Broker or to a website ?
You can advertise for free to sell your Car at free4u.info
Professor Subhashish Chattopadhyay is providing a Social Service for all in Bangalore, to advertise for Free
If you are looking for Organ Donation, where do you ask ? Where do you want to put up your requirements ? Do you give costly ads ?
You can advertise or Post Classifieds for free at free4u.info
Professor Subhashish Chattopadhyay is providing a Social Service for all in Bangalore, to advertise for Free. Post all kinds of Classified ads and Requirements for FREE.
If you are a Tutor, or a Shopkeeper, or a Teacher, or a Cook, or a Gardener, or a Dog Trainer ….. or something something something….. How can you afford costly ads ? Post your requirements for free at free4u.info Advertise yourself free at free4u.info Doing a garage sell …. Tell all for free at free4u.info
Looking for a Nanny ? You can get Nannys in free4u.info
Nannys looking for jobs ? Want children to take care ? You get the child and Parents in free4u.info
Professor Subhashish Chattopadhyay is providing a Social Service for all in Bangalore, to advertise for Free. Post all kinds of Classified ads and Requirements for FREE. Following Categories and Subcategories will surely help you. This is not an exhaustive list. You can give general requirements as well. Post all your skills. Post all your needs. Looking for a job ? You can post your profile as well.
Some call this as ” Yellow Pages “. free4u.info
Some call this a FREE listing sites free4u.info
–








Bike ( Want to sell your Bike ? Want a Buyer ? Advertise for free at free4u.info )
Many more free pdf e-Books are available at ( such as H C Verma Concepts of Physics Solutions )
–
For more e-Books free pdf download see
–
Chemistry Physics Mathematics personal tuitions ( also Home Tuitions / Coaching by Home Tutor with personal Attention ) are available in the Bannerghatta Road IIM ( south Bangalore ) region.
Contact mokshya@gmail.com
–
Solutions to Solutions Chapter 2 :
🙂
🙂
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
Question 2.1 :
🙂
🙂
🙂
Question 2.2 :
🙂
🙂
Question 2.3 :
🙂
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
xxxxxxxxxxxxxxxxxxxxxxxxxx
The next chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-12-electrochemistry-chapter-3/
!
The previous chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-12-solid-state-chapter-1-physical-chemistry/
!
Standard 11 last chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-11-chemistry-chapter-14-environmental-chemistry/
!
xxxxxxxxxxxxxxxxxxxxxxxxxx
🙂
🙂
Normality of Acids is Molarity X Basicity ( where Basicity is number of H+ ions furnished by each molecule of Acid )
–
Normality of Bases is Molarity X Acidity ( where Acidity is number of OH- ions furnished by each molecule of Base )
🙂
Question 2.4 :
🙂
Gyan
🙂
Question 2.5 :
🙂
Gyan
Clapeyron’s Equation
xxxxxxxxxxxxxxxxxxxxxx
Question 2.6 :
🙂
Gyan
🙂
Question 2.7 :
🙂
Gyan
🙂
Question 2.8 :
🙂
Limitations of Henry’s Law
🙂
Question 2.9 :
🙂
Applications of Henry’s Law
🙂
Question 2.10 :
🙂
Diver’s Bends due to Henry’s Law
🙂
Question 2.11 :
🙂
Gyan Question
🙂
Question 2.12 :
🙂
Gyan Question
🙂
Question 2.13 :
🙂
Question 2.14 :
🙂
Variation of Vapor Pressure of a liquid with temperature is given by Claussius Clapeyrons Equation
🙂
Question 2.15 :
🙂
Gyan Question
🙂
Question 2.16 :
🙂
IIT JEE 1986 Vapor Pressure Problem
🙂
Question 2.17 :
🙂
Gyan Question
🙂
Question 2.18 :
🙂
Gyan Question
🙂
Question 2.19 :
🙂
🙂
Gyan Question
🙂
🙂
Gyan
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
🙂
Question 2.20 :
🙂
xxxxxxxxxxxxxxxxxxxxxxxxxx
The next chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-12-electrochemistry-chapter-3/
!
The previous chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-12-solid-state-chapter-1-physical-chemistry/
!
Standard 11 last chapter Solution is at https://zookeepersblog.wordpress.com/ncert-cbse-standard-11-chemistry-chapter-14-environmental-chemistry/
!
xxxxxxxxxxxxxxxxxxxxxxxxxx
Question 2.21 :
🙂
Question 2.22 :
🙂
Question 2.23 :
🙂
Question 2.24 :
🙂
Question 2.25 :
🙂
Question 2.26 :
🙂
Question 2.27 :
🙂
Question 2.28 :
🙂
Question 2.29 :
🙂
Question 2.30 :
🙂
Question 2.31 :
🙂
Question 2.32 :
🙂
Gyan Question
🙂
Question 2.33 :
🙂
Gyan Question
🙂
Question 2.34
🙂
Gyan Question
🙂
Question 2.35 :
🙂
🙂
Question 2.36 :
🙂
🙂
Question 2.37 :
🙂
🙂
Question 2.38 :
🙂
Question 2.39 :
🙂
Question 2.40 :
Therefore the amount of CaCl2 dissolved is 3.42 gm
🙂
Question 2.41 :
🙂
xxxxxxxxxxxxxxxxx
Surprise Element :
Did you know that IIT JEE 1999 had a Clairaut’s differential equation Question.
🙂
How many IIT JEE Guide and Coaching Institutes you attended covered this ?
Dont forget to learn from SKM Classes South Bangalore
🙂
Almost all processes in body occur in some kind of liquid solutions.
In normal life we rarely come across pure substances. Most of these are mixtures containing two or more pure substances. Their utility or importance in life depends on their composition. For example, the properties of brass (mixture of copper and zinc) are quite different from those of German silver (mixture of copper, zinc and nickel) or bronze (mixture of copper and tin); 1 part per million (ppm) of fluoride ions in water prevents tooth decay, while 1.5 ppm causes the tooth to become mottled and high concentrations of fluoride ions can be poisonous (for example, sodium fluoride is used in rat poison); intravenous injections are always dissolved in water containing salts at particular ionic concentrations that match with blood plasma concentrations and so on.
In this Unit, we will consider mostly liquid solutions and their formation. This will be followed by studying the properties of the solutions, like vapour pressure and colligative properties. We will begin with types of solutions and then various alternatives in which concentrations of a solute can be expressed in liquid solution.
2.1 Types of Solutions
Solutions are homogeneous mixtures of two or more than two components. By homogenous mixture we mean that its composition and properties are uniform throughout the mixture. Generally, the component that is present in the largest quantity is known as solvent. Solvent determines the physical state in which solution exists. One or more components present in the solution other than solvent are called solutes. In this Unit we shall consider only binary solutions (i.e.,consisting of two components). Here each component may be solid, liquid or in gaseous state and are summarised in Table 2.1.
| Types of Solution | Solute | Solvent | Common Examples |
|---|---|---|---|
| Gaseous Solution | Gas | Gas | Mixture of Oxygen and nitrogen gases |
| Liquid | Gas | Chloroform in nitrogen gas | |
| Solid | Gas | Camphor in nitrogen gas | |
| Liquid Solutions | Gas | Liquid | Oxygen dissolve in water |
| Liquid | Liquid | Ethanol dissolved in water | |
| Solid | Liquid | Glucose dissolved in water | |
| Solid Solution | Gas | Solid | Solution of hydrogen in palladium |
| Liquid | Solid | Amalgam of mersury with sodium | |
| Solid | Solid | Copper dissolved in gold |
2.2 Expressing Concentration of Solutions
Composition of a solution can be described by expressing its concentration. The latter can be expressed either qualitatively or quantitatively. For example, qualitatively we can say that the solution is dilute (i.e., relatively very small quantity of solute) or it is concentrated (i.e., relatively very large quantity of solute). But in real life these kinds of description can add to lot of confusion and thus the need for a quantitative description of the solution. There are several ways by which we can describe the concentration of the solution quantitatively.
(i) Mass percentage (w/w): The mass percentage of a component of a solution is defined as:
Mass % of a component = Mass of the component in the solution/Total mass of the solution × 100…………(2.1)
For example, if a solution is described by 10% glucose in water by mass, it means that 10 g of glucose is dissolved in 90 g of water resulting in a 100 g solution. Concentration described by mass percentage is commonly used in industrial chemical applications. For example, commercial bleaching solution contains 3.62 mass percentage of sodium hypochlorite in water.
(ii)Volume percentage (v/v): The volume percentage is defined as:
Volume % of a component = Volume of the component/Total volume of solution × 100………….(2.2)
For example, 10% ethanol solution in water means that 10 mL of ethanol is dissolved in water such that the total volume of the solution is 100 mL. Solutions containing liquids are commonly expressed in this unit. For example, a 35% (v/v) solution of ethylene glycol, an antifreeze, is used in cars for cooling the engine. At this concentration the antifreeze lowers the freezing point of water to 255.4K (–17.6°C).
(iii) Mass by volume percentage (w/v): Another unit which is commonly used in medicine and pharmacy is mass by volume percentage. It is the mass of solute dissolved in 100 mL of the solution.
(iv) Parts per million: When a solute is present in trace quantities, it is convenient to express concentration in parts per million (ppm) and is defined as:
Parts per million = Number of parts of the component/Total number of parts of all components of the solution ×106………(2.3)
As in the case of percentage, concentration in parts per million can also be expressed as mass to mass, volume to volume and mass to volume. A litre of sea water (which weighs 1030 g) contains about 6 × 10 –3 g of dissolved oxygen (O2). Such a small concentration is also expressed as 5.8 g per 106 g (5.8 ppm) of sea water. The concentration of pollutants in water or atmosphere is often expressed in terms of μg mL-1 or ppm.
(v) Mole fraction: Commonly used symbol for mole fraction is x and subscript used on the right hand side of x denotes the component. It is defined as:
Mole fraction of a component = Number of moles of the component/Total number of moles of all the components…………(2.4)
For example, in a binary mixture, if the number of moles of A and B are nA and nB respectively, the mole fraction of A will be
xA =nA/nA + nB………..(2.5)
For a solution containing i number of components, we have:
xi = ni/n1 + n2 + ……. + ni=ni/∑ ni…………(2.6)
It can be shown that in a given solution sum of all the mole fractions is unity, i.e.
x1 + x2 + ……………… + xi = 1………..(2.7)
Mole fraction unit is very useful in relating some physical properties of solutions, say vapour pressure with the concentration of the solution and quite useful in describing the calculations involving gas mixtures.
Example 2.1 Calculate the mole fraction of ethylene glycol (C2H6O2) in a solution containing 20% of C2H6O2 by mass.
Solution
Assume that we have 100 g of solution (one can start with any amount of solution because the results obtained will be the same). Solution will contain 20 g of ethylene glycol and 80 g of water.
Molar mass of C2H6O2 = 12 × 2 + 1 × 6 + 16 × 2 = 62 g mol–1.
Moles of C2H6O2 = 20 g/62 g mol−1 = 0.322 mol
Moles of water = 80 g/18 g mol-1= 4.444 mol
x glycol = moles of C2H6O2/moles of C2 H6 O2 + moles of H2O
=0.322 mol/0.322 mol + 4.444 mol= 0.068
Similarly, xwater =4.444 mol/0.322 mol + 4.444 mol = 0.932
Mole fraction of water can also be calculated as: 1 – 0.068 = 0.932
(vi) Molarity: Molarity (M) is defined as number of moles of solute dissolved in one litre (or one cubic decimetre) of solution,
Molarity = Moles of solute/ Volume of solution in litre………..(2.8)
For example, 0.25 mol L–1 (or 0.25 M) solution of NaOH means that 0.25 mol of NaOH has been dissolved in one litre (or one cubic decimetre).
Example 2.2 Calculate the molarity of a solution containing 5 g of NaOH in 450 mL solution.
Solution
Moles of NaOH = 5g/40 g mol-1 = 0.125 mol
Volume of the solution in litres = 450 mL / 1000 mL L-1
Using equation (2.8),
Molarity = 0.125 mol × 1000 mL L–1/450 mL = 0.278 M
= 0.278 mol L–1
= 0.278 mol dm–3
(vii) Molarity: Molality (m) is defined as the number of moles of the solute per kilogram (kg) of the solvent and is expressed as:
Molality (m) = Moles of solute/ Mass of solvent in kg………(2.9)
For example, 1.00 mol kg–1 (or 1.00 m) solution of KCl means that 1 mol (74.5 g) of KCl is dissolved in 1 kg of water.
Each method of expressing concentration of the solutions has its own merits and demerits. Mass %, ppm, mole fraction and molality are independent of temperature, whereas molarity is a function of temperature. This is because volume depends on temperature and the mass does not.
Example 2.3
Calculate molality of 2.5 g of ethanoic acid (CH3COOH) in 75 g of benzene.
Solution
Molar mass of C2H4O2: 12 × 2 + 1 × 4 + 16 × 2 = 60 g mol–1
Moles of C2H4O2 = 2.5 g/60 g mol −1 = 0.0417 mol
Mass of benzene in kg = 75 g/1000 g kg–1 = 75 × 10–3 kg
Molality of C2H4O2 = Moles of C2H4O2/Kg of benzene = 0.0417 mol× 1000 g Kg-1/75g
=0.556 mol Kg-1
Intext Questions
2.1 Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (CCl4) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
2.2 Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
2.3 Calculate the molarity of each of the following solutions: (a) 30 g of Co(NO3)2. 6H2O in 4.3 L of solution (b) 30 mL of 0.5 M H2SO4 diluted to 500 mL.
2.4 Calculate the mass of urea (NH2CONH2) required in making 2.5 kg of 0.25 molal aqueous solution.
2.5 Calculate (a) molality (b) molarity and (c) mole fraction of KI if the density of 20% (mass/mass) aqueous KI is 1.202 g mL-1.
2.3 Solubility
Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a specified temperature. It depends upon the nature of solute and solvent as well as temperature and pressure. Let us consider the effect of these factors in solution of a solid or a gas in a liquid.
2.3.1 Solubility of a Solid in a Liquid
Every solid does not dissolve in a given liquid. While sodium chloride and sugar dissolve readily in water, naphthalene and anthracene do not. On the other hand, naphthalene and anthracene dissolve readily in benzene but sodium chloride and sugar do not. It is observed that polar solutes dissolve in polar solvents and non polar solutes in non- polar solvents. In general, a solute dissolves in a solvent if the intermolecular interactions are similar in the two or we may say like dissolves like.
When a solid solute is added to the solvent, some solute dissolves and its concentration increases in solution. This process is known as dissolution. Some solute particles in solution collide with the solid solute particles and get separated out of solution. This process is known as crystallisation. A stage is reached when the two processes occur at the same rate. Under such conditions, number of solute particles going into solution will be equal to the solute particles separating out and a state of dynamic equilibrium is reached.
Solute + Solvent → Solution……..(2.10)
At this stage the concentration of solute in solution will remain constant under the given conditions, i.e., temperature and pressure. Similar process is followed when gases are dissolved in liquid solvents. Such a solution in which no more solute can be dissolved at the same temperature and pressure is called a saturated solution. An unsaturated solution is one in which more solute can be dissolved at the same temperature. The solution which is in dynamic equilibrium with undissolved solute is the saturated solution and contains the maximum amount of solute dissolved in a given amount of solvent. Thus, the concentration of solute in such a solution is its solubility.
Earlier we have observed that solubility of one substance into another depends on the nature of the substances. In addition to these variables, two other parameters, i.e., temperature and pressure also control this phenomenon.
Effect of temperature
The solubility of a solid in a liquid is significantly affected by temperature changes. Consider the equilibrium represented by equation 2.10. This, being dynamic equilibrium, must follow Le Chateliers Principle. In general, if in a nearly saturated solution, the dissolution process is endothermic (ΔsolH > 0), the solubility should increase with rise in temperature and if it is exothermic (Δsol H > 0) the solubility should decrease. These trends are also observed experimentally.
Effect of pressure
Pressure does not have any significant effect on solubility of solids in liquids. It is so because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.
2.3.2 Solubility of a Gas in a Liquid
Many gases dissolve in water. Oxygen dissolves only to a small extent in water. It is this dissolved oxygen which sustains all aquatic life. On the other hand, hydrogen chloride gas (HCl) is highly soluble in water. Solubility of gases in liquids is greatly affected by pressure and temperature. The solubility of gases increase with increase of pressure. For solution of gases in a solvent, consider a system as shown in Fig. 2.1 (a). The lower part is solution and the upper part is gaseous system at pressure p and temperature T. Assume this system to be in a state of dynamic equilibrium, i.e., under these conditions rate of gaseous particles entering and leaving the solution phase is the same. Now increase the pressure over the solution phase by compressing the gas to a smaller volume [Fig. 2.1 (b)]. This will increase the number of gaseous particles per unit volume over the solution and also the rate at which the gaseous particles are striking the surface of solution to enter it. The solubility of the gas will increase until a new equilibrium is reached resulting in an increase in the pressure of a gas above the solution and thus its solubility increases.
–
Henry was the first to give a quantitative relation between pressure and solubility of a gas in a solvent which is known as Henry’s law. The law states that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the pressure of the gas. Dalton, a contemporary of Henry, also concluded independently that the solubility of a gas in a liquid solution is a function of partial pressure of the gas. If we use the mole fraction of a gas in the solution as a measure of its solubility, then it can be said that the mole fraction of gas in the solution is proportional to the partial pressure of the gas over the solution. The most commonly used form of Henry’s law states that “the partial pressure of the gas in vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution” and is expressed as:
p = KHx……….(2.11)
Here KH is the Henry’s law constant. If we draw a graph between partial pressure of the gas versus mole fraction of the gas in solution, then we should get a plot of the type as shown in Fig. 2.2.
–
Different gases have different KH values at the same temperature (Table 2.2).This suggests that KH is a function of the nature of the gas.
| Gas | Temperature/K | KH/kbar | Gas | Temperature/K | KH/kbar |
|---|---|---|---|---|---|
| He | 293 | 144.97 | Argon | 298 | 40.3 |
| H2 | 293 | 69.16 | CO2 | 298 | 1.67 |
| N2 | 293 | 76.48 | Formaldehyde | 298 | 1.83×10-5 |
| N2 | 293 | 88.84 | Formaldehyde | 298 | 1.83×10-5 |
| O2 | 293 | 88.84 | Methane | 298 | 0.413 |
| O2 | 303 | 46.82 | Vinyl Chloride | 298 | 0.611 |
It is obvious from equation (2.11) that higher the value of KH at a given pressure, the lower is the solubility of the gas in the liquid. It can be seen from Table 2.2 that KH values for both N2 and O2 increase with increase of temperature indicating that the solubility of gases increases with decrease of temperature. It is due to this reason that aquatic species are more comfortable in cold waters rather than in warm waters.
Example 2.4 If N2 gas is bubbled through water at 293 K, how many millimoles of N2 gas would dissolve in 1 litre of water. Assume that N2 exerts a partial pressure of 0.987 bar. Given that Henry’s law constant for N2 at 293 K is 76.48 kbar.
Solution
The solubility of gas is related to the mole fraction in aqueous solution. The mole fraction of the gas in the solution is calculated by applying Henry’s law. Thus:
x(Nitrogen) = p (nitrogen)/KH = 0.987bar/76,480 bar =1.29 × 10-5
As 1 litre of water contains 55.5 mol of it, therefore if n represents number of moles of N2 in solution,
x(Nitrogen) = n mol/ n mol + 55.5 mol =n/55.5= 1.29×10-5
(n in denominator is neglected as it is < < 55.5)
Thus n = 1.29 × 10–5 × 55.5 mol = 7.16 × 10–4 mol
=7.16×10−4 mol × 1000 mol/1 mol = 0.716 mmol
Henry’s law finds several applications in industry and explains some biological phenomena. Notable among these are:
• To increase the solubility of CO2 in soft drinks and soda water, the bottle is sealed under high pressure.
• Scuba divers must cope with high concentrations of dissolved gases while breathing air at high pressure underwater. Increased pressure increases the solubility of atmospheric gases in blood. When the divers come towards surface, the pressure gradually decreases. This releases the dissolved gases and leads to the formation of bubbles of nitrogen in the blood. This blocks capillaries and creates a medical condition known as bends, which are painful and dangerous to life.
To avoid bends, as well as, the toxic effects of high concentrations of nitrogen in the blood, the tanks used by scuba divers are filled with air diluted with helium (11.7% helium, 56.2% nitrogen and 32.1% oxygen).
• At high altitudes the partial pressure of oxygen is less than that at the ground level. This leads to low concentrations of oxygen in the blood and tissues of people living at high altitudes or climbers. Low blood oxygen causes climbers to become weak and unable to think clearly, symptoms of a condition known as anoxia.
Effect of Temperature
Solubility of gases in liquids decreases with rise in temperature. When dissolved, the gas molecules are present in liquid phase and the process of dissolution can be considered similar to condensation and heat is evolved in this process. We have learnt in the last Section that dissolution process involves dynamic equilibrium and thus must follow Le Chatelier’s Principle. As dissolution is an exothermic process, the solubility should decrease with increase of temperature.
Intext Questions
2.6 H2S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H2S in water at STP is 0.195 m, calculate Henry’s law constant.
2.7 Henry’s law constant for CO2 in water is 1.67×108 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at 298 K.
2.4 Vapour Pressure of Liquid Solution
Liquid solutions are formed when solvent is a liquid. The solute can be a gas, a liquid or a solid. Solutions of gases in liquids have already been discussed in Section 2.3.2. In this Section, we shall discuss the solutions of liquids and solids in a liquid. Such solutions may contain one or more volatile components. Generally, the liquid solvent is volatile. The solute may or may not be volatile. We shall discuss the properties of only binary solutions, that is, the solutions containing two components, namely, the solutions of (i) liquids in liquids and (ii) solids in liquids.
2.4.1 Vapour pressure of Liquid – Liquid Solutions
Let us consider a binary solution of two volatile liquids and denote the two components as 1 and 2. When taken in a closed vessel, both the components would evaporate and eventually an equilibrium would be established between vapour phase and the liquid phase. Let the total vapour pressure at this stage be ptotal and p1 and p2be the partial vapour pressures of the two components 1 and 2 respectively. These partial pressures are related to the mole fractions x1 and x2 of the two components 1 and 2 respectively.
The French chemist, Francois Marte Raoult (1886) gave the quantitative relationship between them. The relationship is known as the Raoult’s law which states that for a solution of volatile liquids, the partial vapour pressure of each component in the solution
is directly proportional to its mole fraction.
Thus, for component 1
p1 ∝ x1
and
p1 = p01 x1………(2.12)
where p01 is the vapour pressure of pure component 1 at the same temperature.
Similarly, for component 2
p2 = p02° x2…………(2.13)
where p02° represents the vapour pressure of the pure component 2. According to Dalton’s law of partial pressures, the total pressure
( ptotal ) over the solution phase in the container will be the sum of the partial pressures of the components of the solution and is given as:
ptotal = p1 + p2……….(2.14)
Substituting the values of p1 and p2, we get
ptotal = x1 p10 + x2 p20
= (1 – x2) p10 + x2 p20………..(2.15)
= p10 + (p20 – p10 ) x2………….(2.16)
Following conclusions can be drawn from equation (2.16).
(i) Total vapour pressure over the solution can be related to the mole fraction of any one component.
(ii) Total vapour pressure over the solution varies linearly with the mole fraction of component 2.
(iii) Depending on the vapour pressures of the pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1.
A plot of p1 or p2 versus the mole fractions x1 and x2 for a solution gives a linear plot as shown in Fig. 2.3. These lines (I and II) pass through the point and respectively when x1 and x2 equal unity. Similarly the plot (line III) of ptotal versus x2 is also linear (Fig. 2.3). The minimum value of ptotal is p1 and the maximum value is p2 , assuming that component 1 is less volatile than component 2, i.e., p1 < p2 .
–
The composition of vapour phase in equilibrium with the solution is determined by the partial pressures of the components. If y1 and y2 are the mole fractions of the components 1 and 2 respectively in the vapour phase then, using Dalton’s law of partial pressures:
p1 = y 1 ptotal………………(2.17)
p2 = y 2 ptotal………………(2.18)
In general
pi = y i ptotal……………….(2.19)
Example 2.5
Vapour pressure of chloroform (CHCl3) and dichloromethane (CH2Cl2) at 298 K are 200 mm Hg and 415 mm Hg respectively. (i) Calculate the vapour pressure of the solution prepared by mixing 25.5 g of CHCl3 and 40 g of CH2Cl2 at 298 K and, (ii) mole fractions of each component in vapour phase.
Solution
(i) Molar mass of CH2Cl2 = 12 × 1 + 1 × 2 + 35.5 × 2 = 85 g mol–1
Molar mass of CHCl3 = 12 × 1 + 1 × 1 + 35.5 × 3 = 119.5 g mol-1
Moles of CH2Cl2 = 40 g/85 g mol −1 = 0.47 mol
Moles of CHCl3 = 25.5g/ 119.5 g mol-1 = 0.213 mol
Total number of moles = 0.47 + 0.213 = 0.683 mol
xCH2Cl2 = 0.47 mol/0.683 mol = 0.688
xCHCl3 = 1.00 – 0.683 = 0.312
Using equation (2.16),
ptotal = p1°+(p2° – p1°)x2 = 200 + (415 – 200) 0.688
=200 + 147.9 = 347.9 mmHg
(ii)Using the relation (2.17), yi = pi/ptotal, we can calculate the mole fraction of the components in gas phase (yi).
pCH2Cl2 = 0.688 × 415 mm Hg = 285.5 mm Hg
pCHCl3 = 0.312 × 200 mm Hg = 62.4 mm Hg
yCH2Cl2 = 285.5 mm Hg/347.9 mm Hg = 0.82
yCHCl3 = 62.4 mm Hg/347.9 mm Hg = 0.18
Note: Since, CH2Cl2 is a more volatile component than CHCl3, [ p0 CH2 Cl2 = 415 mm Hg and p CHCl3 = 200 mm Hg] and the vapour phase is also richer in CH2Cl2 [ yCH2Cl2 = 0.82 and yCHCl3 = 0.18], it may thus be concluded that at equilibrium, vapour phase will be always rich in the component which is more volatile.
2.4.2 Raoult’s Law as a special case of Henry’s Law
According to Raoult’s law, the vapour pressure of a volatile component in a given solution is given by pi = xipi0. In the solution of a gas in a liquid, one of the components is so volatile that it exists as a gas and we have already seen that its solubility is given by Henry’s law which states that
p = KH x.
If we compare the equations for Raoult’s law and Henry’s law, it can be seen that the partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. Only the proportionality constant KH differs from p1 . Thus, Raoult’s law becomes a special case of Henry’s law in which KH becomes equal to p1 .
2.4.3 Vapour Pressure of Solutions of Solids in Liquids
Another important class of solutions consists of solids dissolved in liquid, for example, sodium chloride, glucose, urea and cane sugar in water and iodine and sulphur dissolved in carbon disulphide. Some physical properties of these solutions are quite different from those of pure solvents. For example, vapour pressure. We have learnt in Unit 5, Class XI, that liquids at a given temperature vapourise and under equilibrium conditions the pressure exerted by the vapours of the liquid over the liquid phase is called vapour pressure [Fig. 2.4 (a)]. In a pure liquid the entire surface is occupied by the molecules of the liquid. If a non-volatile solute is added to a solvent to give a solution [Fig. 2.4.(b)], the vapour pressure of the solution is solely from the solvent alone. This vapour pressure of the solution at a given temperature is found to be lower than the vapour pressure of the pure solvent at the same temperature. In the the solution, the surface has both solute and solvent molecules; thereby the fraction of the of the surface covered by the solvent molecules gets reduced. Consequently, the number of solvent molecules escaping from the surface is correspondingly reduced, thus, the vapour pressure is also reduced.
–
The decrease in the vapour pressure of solvent depends on the quantity of non-volatile solute present in the solution, irrespective of its nature. For example, decrease in the vapour pressure of water by adding 1.0 mol of sucrose to one kg of water is nearly similar to that produced by adding 1.0 mol of urea to the same quantity of water at the same temperature.
Raoult’s law in its general form can be stated as, for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
In a binary solution, let us denote the solvent by 1 and solute by
2. When the solute is non-volatile, only the solvent molecules are present in vapour phase and contribute to vapour pressure. Let p1 be the vapour pressure of the solvent, x1 be its mole fraction, pi be its vapour pressure in the pure state. Then according to Raoult’s law
p1 ∝ x1
and p1 = x1 p1……….(2.20)
The proportionality constant is equal to the vapour pressure of pure solvent, p1 . A plot between the vapour pressure and the mole fraction of the solvent is linear (Fig. 2.5).
2.5 Ideal and Non-ideal Solutions
Liquid-liquid solutions can be classified into ideal and non-ideal solutions on the basis of Raoult’s law.
2.5.1 Ideal Solutions
The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e.,
ΔmixH = 0, ΔmixV = 0…………(2.21)
It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of volumes of the two components. At molecular level, ideal behaviour of the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal solution. A perfectly ideal solution is rare but some solutions are nearly ideal in behaviour. Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc. fall into this category.
2.5.2 Non-ideal Solutions
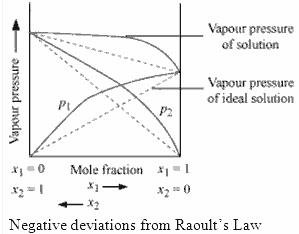
When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution. The vapour pressure of such a solution is either higher or lower than that predicted by Raoult’s law (equation 2.16). If it is higher, the solution exhibits positive deviation and if it is lower, it exhibits negative deviation from Raoult’s law. The plots of vapour pressure as a function of mole fractions for such solutions are shown in Fig. 2.6.
The cause for these deviations lie in the nature of interactions at the molecular level. In case of positive deviation from Raoult’s law, A-B interactions are weaker than those between A-A or B-B, i.e., in this case the intermolecular attractive forces between the solute-solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. This means that in such solutions, molecules of A (or B) will find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation. Mixtures of ethanol and acetone behave in this manner. In pure ethanol, molecules are hydrogen bonded. On adding acetone, its molecules get in between the host molecules and break some of the hydrogen bonds between them. Due to weakening of interactions, the solution shows positive deviation from Raoult’s law [Fig. 2.6 (a)]. In a solution formed by adding carbon disulphide to acetone, the dipolar interactions between solute-solvent molecules are weaker than the respective interactions among the solute-solute and solvent-solvent molecules. This solution also shows positive deviation.
–
In case of negative deviations from Raoult’s law, the intermolecular attractive forces between A-A and B-B are weaker than those between A-B and leads to decrease in vapour pressure resulting in negative deviations. An example of this type is a mixture of phenol and aniline. In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar molecules. Similarly, a mixture of chloroform and acetone forms a solution with negative deviation from Raoult’s law. This is because chloroform molecule is able to form hydrogen bond with acetone molecule as shown.
–
This decreases the escaping tendency of molecules for each component and consequently the vapour pressure decreases resulting in negative deviation from Raoult’s law [Fig. 2.6. (b)].
Some liquids on mixing, form azeotropes which are binary mixtures having the same composition in liquid and vapour phase and boil at a constant temperature. In such cases, it is not possible to separate the components by fractional distillation. There are two types of azeotropes called minimum boiling azeotrope and maximum boiling azeotrope. The solutions which show a large positive deviation from Raoult’s law form minimum boiling azeotrope at a specific composition. For example, ethanol-water mixture (obtained by fermentation of sugars) on fractional distillation gives a solution containing approximately 95% by volume of ethanol. Once this composition, known as azeotrope composition, has been achieved, the liquid and vapour have the same composition, and no further separation occurs.
The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition. Nitric acid and water is an example of this class of azeotrope. This azeotrope has the approximate composition, 68% nitric acid and 32% water by mass, with a boiling point of 393.5 K.
Intext Question
2.8 The vapour pressure of pure liquids A and B are 450 and 700 mm Hg respectively, at 350 K . Find out the composition of the liquid mixture if total vapour pressure is 600 mm Hg. Also find the composition of the vapour phase.
2.6 Colligative Properties and Determination of molar mass
We have learnt in Section 2.4.3 that the vapour pressure of solution decreases when a non-volatile solute is added to a volatile solvent. There are many properties of solutions which are connected with this decrease of vapour pressure. These are: (1) relative lowering of vapour pressure of the solvent (2) depression of freezing point of the solvent (3) elevation of boiling point of the solvent and (4) osmotic pressure of the solution. All these properties depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution. Such properties are called colligative properties (colligative: from Latin: co means together, ligare means to bind). In the following Sections we will discuss these properties one by one.
2.6.1 Relative Lowering of Vapour Pressure
We have learnt in Section 2.4.3 that the vapour pressure of a solvent in solution is less than that of the pure solvent. Raoult established that the lowering of vapour pressure depends only on the concentration of the solute particles and it is independent of their identity. The equation (2.20) given in Section 2.4.3 establishes a relation between vapour pressure of the solution, mole fraction and vapour pressure of the solvent, i.e.,
p1 = x1 p10………..(2.22)
The reduction in the vapour pressure of solvent (Δp1) is given as:
Δp1 = p1° – p1 = p1° – p1° x1
= p1o (1 – x1)……..(2.23)
Knowing that x2 = 1 – x1, equation (2.23) reduces to
Δp1 = x2 p1°………. (2.24)
In a solution containing several non-volatile solutes, the lowering of the vapour pressure depends on the sum of the mole fraction of different solutes.
Equation (2.24) can be written as
Δp1/p1° = (p1° − p1)/p1° = x2………..(2.25)
The expression on the left hand side of the equation as mentioned earlier is called relative lowering of vapour pressure and is equal to the mole fraction of the solute. The above equation can be written as:
p1° – p1/p1° = n2 n1+n2(since x2 = n2/n1 + n2………..(2.26)
Here n1 and n2 are the number of moles of solvent and solute respectively present in the solution. For dilute solutions n2<< n1, hence neglecting n2 in the denominator we have
p1°-p1/p1° = n2/n1…………(2.27)
or p1°-p1/p1° = w2×M1/M2 ×w1…………(2.28)
Here w1 and w2 are the masses and M1 and M2 are the molar masses of the solvent and solute respectively.
From this equation (2.28), knowing all other quantities, the molar mass of solute (M2) can be calculated.
Example 2.6
The vapour pressure of pure benzene at a certain temperature is 0.850 bar. A non-volatile, non-electrolyte solid weighing 0.5 g when added to 39.0 g of benzene (molar mass 78 g mol-1). Vapour pressure of the solution, then, is 0.845 bar. What is the molar mass of the solid substance?
Solution
The various quantities known to us are as follows:
p10 = 0.850 bar; p = 0.845 bar; M1 = 78 g mol–1; w2 = 0.5 g; w1 = 39 g
Substituting these values in equation (2.28), we get
0.5 g × 78 g mol –1
0.850 bar – 0.845 bar/0.850 bar = 0.5g×78g mol-1 /M2 × 39 g
Therefore, M2 = 170 g mol–1
2.6.2 Elevation of Boiling Point
We have learnt in Unit 5, Class XI, that the vapour pressure of a liquid increases with increase of temperature. It boils at the temperature at which its vapour pressure is equal to the atmospheric pressure. For example, water boils at 373.15 K (100° C) because at this temperature the vapour pressure of water is 1.013 bar (1
atmosphere). We have also learnt in the last section that vapour pressure of the solvent decreases in the presence of non-volatile solute. Fig. 2.7 depicts the variation of vapour pressure of the pure solvent and solution as a function of temperature. For example, the vapour pressure of an aqueous solution of sucrose is less than 1.013 bar at 373.15 K. In order to make this solution boil, its vapour pressure must be increased to 1.013 bar by raising the temperature above the boiling temperature of the pure solvent (water). Thus, the boilingpoint of a solution is always higher than that of the boiling point of the pure solvent in which the solution is prepared as shown in Fig. 2.7. Similar to lowering of vapour pressure, the elevation of boiling point also depends on the number of solute molecules rather than their nature. A solution of 1 mol of sucrose in 1000 g of water boils at 373.52 K at one atmospheric pressure.
–
Let T0b be the boiling point of pure solvent and Tb be the boiling point of solution. The increase in the boiling point ΔTb = Tb − Tb is known as elevation of boiling point.
Experiments have shown that for dilute solutions the elevation of boiling point (ΔTb) is directly proportional to the molal concentration of
the solute in a solution. Thus
ΔTb ∝ m…………..(2.29)
or
ΔTb = Kbm………….(2.30)
Here m (molality) is the number of moles of solute dissolved in 1 kg of solvent and the constant of proportionality, Kb is called Boiling Point.
Elevation Constant or Molal Elevation Constant (Ebullioscopic Constant). The unit of Kb is K kg mol-1. Values of Kb for some common solvents are given in Table 2.3. If w2 gram of solute of molar mass M2 is dissolved in w1 gram of solvent, then molality, m of the solution is given by the expression:
m = w2/M2/1000 × w2 = 1000 × w2 M2 × w1…………(2.31)
Substituting the value of molality in equation (2.30) we get
ΔTb = Kb × 1000 × w2/M2 × w1……….(2.32)
M2 = 1000 × w2 × Kb/ΔTb × w1 (2.33)
Thus, in order to determine M2, molar mass of the solute, known mass of solute in a known mass of the solvent is taken and ΔTb is determined experimentally for a known solvent whose Kb value is known.
Example 2.7
18 g of glucose, C6H12O6, is dissolved in 1 kg of water in a saucepan. At what temperature will water boil at 1.013 bar? Kb for water is 0.52K kg mol-1.
solution
Moles of glucose = 18 g/ 180 g mol–1 = 0.1 mol
Number of kilograms of solvent = 1 kg
Thus molality of glucose solution = 0.1 mol kg-1
For water, change in boiling point
Ä Tb = Kb × m = 0.52 K kg mol–1 × 0.1 mol kg–1 = 0.052 K
Since water boils at 373.15 K at 1.013 bar pressure, therefore, the boiling point of solution will be 373.15 + 0.052 = 373.202 K.
Example 2.8
The boiling point of benzene is 353.23 K. When 1.80 g of a non-volatile solute was dissolved in 90 g of benzene, the boiling point is raised to 354.11 K. Calculate the molar mass of the solute. Kb for benzene is 2.53 K kg mol–1
Solution
The elevation ( Tb) in the boiling point = 354.11 K – 353. 23 K = 0.88 K
Substituting these values in expression (2.33) we get
M2=2.53 K kg mol –1 × 1.8 g × 1000 g kg –1/0.88 K × 90 g = 58 g mol–1
Therefore, molar mass of the solute, M2 = 58 g mol–1
2.6.3 Depression of freezing
The lowering of vapour pressure of a solution causes a lowering of the of Freezing freezing point compared to that of the pure solvent (Fig. 2 8). We know that at the freezing point of a substance, the solid phase is in dynamic equilibrium with the liquid phase. Thus, the freezing point of a substance may be defined as the temperature at which the vapour pressure of the substance in its liquid phase is equal to its vapour pressure in the solid phase. A solution will freeze when its vapour pressure equals the vapour pressure of the pure solid solvent as is clear from Fig. 2.8. According to Raoult’s law, when a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases.
–
Let Tf° be the freezing point of pure solvent and Tf be its freezing point when non-volatile solute is dissolved in it. The decrease in freezing point.
ΔTf = Tf° − Tf is known as depression in freezing point.
Similar to elevation of boiling point, depression of freezing point (ΔTf) for dilute solution (ideal solution) is directly proportional to molality,
m of the solution. Thus,
ΔTf∝ m
or
ΔTf = Kfm……….(2.34)
The proportionality constant, Kf, which depends on the nature of the solvent is known as Freezing Point
Depression Constant or Molal Depression Constant or Cryoscopic Constant. The unit of Kf is K kg mol-1. Values of Kf for some common solvents are listed in Table 2.3. If w2 gram of the solute having molar mass as M2, present in w1 gram of solvent, produces the depression in freezing point ΔTf of the solvent then molality of the solute is given by the equation (2.31).
m = w2 / M2/w1/1000………(2.31)
Substituting this value of molality in equation (2.34) we get:
ΔTf = K f × w2 / M2/w1/1000
ΔTf = Kf × w2 × 1000………. (2.35)
M2 /w1
M2 = Kf × w2 × 1000/ΔTf × w1 (2.36)
Thus for determining the molar mass of the solute we should know the quantities w1, w2, ΔTf, along with the molal freezing point depression constant.
The values of Kf and Kb, which depend upon the nature of the solvent, can be ascertained from the following relations.
Kf= R × M1 × Tf2/ 1000 × Δ fus H…………. (2.37)
Kb= R × M1 × Tb2/1000 × Δvap H (2.38)
Here the symbols R and M1 stand for the gas constant and molar mass of the solvent, respectively and Tf and Tb denote the freezing point and the boiling point of the pure solvent respectively in kelvin. Further, ΔfusH and ΔvapH represent the enthalpies for the fusion and vapourisation of the solvent, respectively.
\
| Solvent | b.p./K | Kb/K kg mol-1 | f.p./K | Kf/K kg mol-1 |
|---|---|---|---|---|
| Water | 373.15 | 0.52 | 273.0 | 1.86 |
| Ethanol | 351.5 | 1.20 | 155.7 | 1.99 |
| Cyclohexane | 353.74 | 2.79 | 279.55 | 20.00 |
| Benzene | 353.3 | 2.53 | 278.6 | 5.12 |
| Chloroform | 334 | 3.63 | 209.6 | 4.79 |
| Carbon tetrachloride | 350.0 | 5.03 | 250.5 | 31.8 |
| Carbon disulphide | 319.4 | 2.34 | 164.2 | 3.83 |
| Diethyl ether | 307.8 | 2.02 | 156.9 | 1.79 |
| Acetic acid | 391.1 | 2.93 | 290.0 | 3.90 |
Example 2.9
45 g of ethylene glycol (C2H6O2) is mixed with 600 g of water. Calculate (a) the freezing point depression and (b) the freezing point of the solution.
Solution
Depression in freezing point is related to the molality, therefore, the molality moles of ethylene glycol of the solution with respect to ethylene glycol =moles of ethylene glycol/ mass of water in kilogram
Moles of ethylene glycol =45/62 g mol-1=0.73 mol
Mass of water in kg =600g/1000g kg-1 = 0.6 kg
Hence molality of ethylene glycol = 0.73mol/0.60kg = 1.2 mol kg –1
Therefore freezing poin depression,
Ä Tf = 1.86 K kg mol–1 × 1.2 mol kg –1 = 2.2 K
Freezing point of the aqueous solution = 273.15 K – 2.2 K = 270.95 K
Example 2.10 1.00 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0.40 K. The freezing point depression constant of benzene is 5.12 K kg mol–1. Find the molar mass of the solute.
Solution
Substituting the values of various terms involved in equation (2.36) we get,
M2 = 5.12 K kg mol−1 × 1.00 g × 1000 g kg−1/0.40 × 50 g = 256 g mol-1
Thus, molar mass of the solute = 256 g mol-1
2.6.4 Osmosis and Osmotic Pressure
There are many phenomena which we observe in nature or at home. For example, raw mangoes shrivel when pickled in brine (salt water); wilted flowers revive when placed in fresh water, blood cells collapse when suspended in saline water, etc. If we look into these processes we find one thing common in all, that is, all these substances are bound by membranes. These membranes can be of animal or vegetable origin and these occur naturally such as pig’s bladder or parchment or can be synthetic such as cellophane. These membranes appear to be continuous sheets or films, yet they contain a network of submicroscopic holes or pores. Small solvent molecules, like water, can pass through these holes but the passage of bigger molecules like solute is hindered. Membranes having this kind of properties are known as semipermeable membranes (SPM).
–
Assume that only solvent molecules can pass through these semi- permeable membranes. If this membrane is placed between the solvent and solution as shown in Fig. 2.9, the solvent molecules will flow through the membrane from pure solvent to the solution. This process of flow of the solvent is called osmosis.
The flow will continue till the equilibrium is attained. The flow of the solvent from its side to solution side across a semipermeable membrane can be stopped if some extra pressure is applied on the solution. This pressure that just stops the flow of solvent is called osmotic pressure of the solution. The flow of solvent from dilute solution to the concentrated solution across a semipermeable membrane is due to osmosis. The important point to be kept in mind is that solvent molecules always flow from lower concentration to higher concentration of solution. The osmotic pressure has been found to depend on the concentration of the solution.
–
The osmotic pressure of a solution is the excess pressure that must be applied to a solution to prevent osmosis, i.e., to stop the passage of solvent molecules through a semipermeable membrane into the solution. This is illustrated in Fig. 2.10. Osmotic pressure is a colligative property as it depends on the number of solute molecules and not on their identity. For dilute solutions, it has been found experimentally that osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:
Π=CRT………(2.39)
Here ð is the osmotic pressure and R is the gas constant.
Π = (n2 /V) R T………..(2.40)
Here V is volume of a solution in litres containing n2 moles of solute. If w2 grams of solute, of molar mass, M2 is present in the solution, then n2 = w2 / M2 and we can write,
Π V= w2R T/M2……………….(2.41)
or
M2 = w2R T/Π V…………….(2.42)
Thus, knowing the quantities w2, T,Π and V we can calculate the molar mass of the solute.
Measurement of osmotic pressure provides a other method of determining molar masses of solutes. This method is widely used to determine molar masses of proteins, polymers and othermacromolecules. The osmotic pressure method has the advantage over other methods as pressure measurement is around the room temperature and the molarity of the solution is used instead of molality. As compared to other colligative properties, its magnitude is large even for very dilute solutions. The technique of osmotic pressure for determination of molar mass of solutes is particularly useful for biomolecules as they are generally not stable at higher temperatures and polymers have poor solubility.
Two solutions having same osmotic pressure at a given temperature are called isotonic solutions. When such solutions are separated by semipermeable membrane no osmosis occurs between them. For example, the osmotic pressure associated with the fluid inside the blood cell is equivalent to that of 0.9% (mass/ volume) sodium chloride solution, called normal saline solution and it is safe to inject intravenously. On the other hand, if we place the cells in a solution containing more than 0.9% (mass/volume) sodium chloride, water will flow out of the cells and they would shrink. Such a solution is called hypertonic. If the salt concentration is less than 0.9% (mass/volume), the solution is said to be hypotonic. In this case, water will flow into the cells if placed in this solution and they would swell.
Example 2.11
200 cm3 of an aqueous solution of a protein contains 1.26 g of the protein. The osmotic pressure of such a solution at 300 K is found to be 2.57 × 10-3 bar. Calculate the molar mass of the protein.
Solution
The various quantities known to us are as follows: Π = 2.57 × 10–3 bar,
V = 200 cm3 = 0.200 litre
T = 300 K
R = 0.083 L bar mol-1 K-1
Substituting these values in equation (2.42) we get
M2 = 1.26 g × 0.083 L bar K−1 mol−1 × 300 K / 2.57×10−3 bar × 0.200 L = 61,022 g mol-1
The phenomena mentioned in the beginning of this section can be explained on the basis of osmosis. A raw mango placed in concentrated salt solution loses water via osmosis and shrivel into pickle. Wilted flowers revive when placed in fresh water. A carrot that has become limp because of water loss into the atmosphere can be placed into the water making it firm once again. Water will move into them through osmosis. When placed in water containing less than 0.9% (mass/volume) salt, blood cells collapse due to loss of water by osmosis. People taking a lot of salt or salty food experience water retention in tissue cells and intercellular spaces because of osmosis. The resulting puffiness or swelling is called edema. Water movement from soil into plant roots and subsequently into upper portion of the plant is partly due to osmosis. The preservation of meat by salting and of fruits by adding sugar protects against bacterial action. Through the process of osmosis, a bacterium on salted meat or candid fruit loses water, shrivels and dies.
2.6.5 Reverse Osmosis and Water Purification
The direction of osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution side. That is, now the pure solvent flows out of the solution through the semi permeable membrane. This phenomenon is called reverse osmosis and is of great practical utility. Reverse osmosis is used in desalination of sea water. A schematic set up for the process is shown in Fig. 2.11. When pressure more than osmotic pressure is applied, pure water is squeezed out of the sea water through the membrane. A variety of polymer membranes are available for this purpose.
–
The pressure required for the reverse osmosis is quite high. A workable porous membrane is a film of cellulose acetate placed over a suitable support. Cellulose acetate is permeable to water but impermeable to impurities and ions present in sea water. These days many countries use desalination plants to meet their potable water requirements.
Intext Question
2.9 Vapour pressure of pure water at 298 K is 23.8 mm Hg. 50 g of urea (NH2CONH2) is dissolved in 850 g of water. Calculate the vapour pressure
of water for this solution and its relative lowering.
2.10 Boiling point of water at 750 mm Hg is 99.63°C. How much sucrose is to be added to 500 g of water such that it boils at 100°C.
2.11 Calculate the mass of ascorbic acid (Vitamin C, C6H8O6) to be dissolved in 75 g of acetic acid to lower its melting point by 1.5°C. Kf = 3.9 K kg mol-1.
2.12 Calculate the osmotic pressure in pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 185,000 in 450 mL of water at 37°C.
2.7 Abnormal Molar Masses
We know that ionic compounds when dissolved in water dissociate into cations and anions. For example, if we dissolve one mole of KCl (74.5 g) in water, we expect one mole each of K+ and Cl– ions to be released in the solution. If this happens, there would be two moles of particles in the solution. If we ignore interionic attractions, one mole of KCl in one kg of water would be expected to increase the boiling point by 2 × 0.52 K = 1.04 K. Now if we did not know about the degree of dissociation, we could be led to conclude that the mass of 2 mol particles is 74.5 g and the mass of one mole of KCl would be 37.25 g. This brings into light the rule that, when there is dissociation of solute into ions, the experimentally determined molar mass is always lower than the true value.
Molecules of ethanoic acid (acetic acid) dimerise in benzene due to hydrogen bonding. This normally happens in solvents of low dielectric constant. In this case the number of particles is reduced due to dimerisation. Association of molecules is depicted as follows:
–
It can be undoubtedly stated here that if all the molecules of ethanoic acid associate in benzene, then ΔTb or ΔTf for ethanoic acid will be half of the normal value. The molar mass calculated on the basis of this ΔTb or ΔTf will, therefore, be twice the expected value. Such a molar mass that is either lower or higher than the expected or normal value is called as abnormal molar mass.
In 1880 van’t Hoff introduced a factor i, known as the van’t Hoff factor, to account for the extent of dissociation or association. This factor i is defined as:
i = Normal molar mass/ Abnormal molar mass
= Observed colligative property / Calculated colligative property
i =(Total number of moles of particles after association/dissociation)/(Number of moles of particles before association/dissociation)
Here abnormal molar mass is the experimentally determined molar mass and calculated colligative properties are obtained by assuming that the non-volatile solute is neither associated nor dissociated. In case of association, value of i is less than unity while for dissociation it is greater than unity. For example, the value of i for aqueous KCl solution is close to 2, while the value for ethanoic acid in benzene is nearly 0.5.
Inclusion of van’t Hoff factor modifies the equations for colligative properties as follows:
Relative lowering of vapour pressure of solvent,
(p1° – p1)/p1° = i.(n2)/n1
Elevation of Boiling point, ΔTb = i Kb m
Depression of Freezing point, ΔTf = i Kf m
Osmotic pressure of solution, Π = i n2 R T / V
Table 2.4 depicts values of the factor, i for several strong electrolytes. For KCl, NaCl and MgSO4, i approach 2 as the solution becomes very dilute. As expected, the value of i gets close to 3 for K2SO4.
| Salt | *Value of i | van’t Hoff Factor i for complete dissociation of solute | ||
|---|---|---|---|---|
| 0.1m | 0.01m | 0.001m | ||
| NaCl | 1.87 | 1.94 | 1.97 | 2.00 |
| KCl | 1.85 | 1.94 | 1.98 | 2.00 |
| MgSO4 | 1.21 | 1.53 | 1.82 | 2.00 |
| K2SO4 | 2.32 | 2.70 | 2.84 | 3.00 |
Example 2.12
2 g of benzoic acid (C6H5COOH) dissolved in 25 g of benzene shows a depression in freezing point equal to 1.62 K. Molal depression constant for benzene is 4.9 K kg mol–1. What is the percentage association of acid if it forms dimer in solution?
Solution
The given quantities are:w2 = 2 g; Kf = 4.9 K kg mol–1 w1 = 25 g,
Ä Tf = 1.62 K
Substituting these values in equation (2.36) we get:
M2 = 4.9 K kg mol–1 × 2g × 1000 g kg –1/25 g × 1.62 K = 241.98 g mol–1
Thus, experimental molar mass of benzoic acid in benzene is
= 241.98 g mol–1
Now consider the following equilibrium for the acid:
2 C6H5COOH (C6H5COOH)2
If x represents the degree of association of the solute then we would have (1 – x ) mol of benzoic acid left in unassociated form and x/2 as associated moles of benzoic acid at equilibrium. correspondingly x/2 as associated moles of benzoic acid at equilibrium.
Therefore, total number of moles of particles at equilibrium is:
= 1−x+x/2 = 1-x/2
Thus, total number of moles of particles at equilibrium equals van’t Hoff factor i.
But i = Normal molar mass / Abnormal molar mass
= 122 g mol-1/241.98 g mol
or x/2 = 1 – 122 /241.98 = 1 – 0.0504 = 0.496
or x = 2 × 0 .496 = 0.992
Therefore, degree of association of benzoic acid in benzene is 99.2 %.
Example 2.13
0.6 mL of acetic acid (CH3COOH), having density 1.06 g mL–1, is dissolved in 1 litre of water. The depression in freezing point observed for this strength of acid was 0.0205°C. Calculate the van’t Hoff factor and the dissociation constant of acid.
Solution
Number of moles of acetic acid = 0.6 ml × 1.06 g mL−1/60 g mol −1 = 0.0106 mol = n
Molality = 0.0106 mol = 0.0106 mol kg–1
Using equation (2.35)
ΔTf = 1.86 K kg mol–1 × 0.0106 mol kg–1 = 0.0197 K
van’t Hoff Factor (i)= Observed freezing point/ Calculate Frezing point =0.0205 K/0.0197 K= 1.041
Acetic acid is a weak electrolyte and will dissociate into two ions:
acetate and hydrogen ions per molecule of acetic acid. If x is the degree of dissociation of acetic acid, then we would have n (1 – x) moles of undissociated acetic acid, nx moles of CH3COO– and nx moles of H+ ions,
–
Thus total moles of particles are: n(1 – x + x + x) = n(1 + x)
i = n (1 + x )/n = 1 + x = 1.041
Thus degree of dissociation of acetic acid = x = 1.041 – 1.000 = 0.041
Then
[CH3COOH] = n(1 – x) 0.0106 (1 – 0.041),
[CH3COO–] = nx = 0.0106 × 0.041, [H+] = nx = 0.0106 × 0.041.
ka=[CH3COO–][H+]/[CH3COOH]=0.0106× 0.041 × 0.0106 × 0.041/0.0106 (1.00 − 0.041)
= 1.86 × 10–5
Summary
A solution is a homogeneous mixture of two or more substances. Solutions are classified as solid, liquid and gaseous solutions. The concentration of a solution is expressed in terms of mole fraction, molarity, molality and in percentages. The dissolution of a gas in a liquid is governed by Henry’s law, according to which, at a given temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas. The vapour pressure of the solvent is lowered by the presence of a non-volatile solute in the solution and this lowering of vapour pressure of the solvent is governed by Raoult’s law, according to which the relative lowering of vapour pressure of the solvent over a solution is equal to the mole fraction of a non-volatile solute present in the solution. However, in a binary liquid solution, if both the components of the solution are volatile then another form of Raoult’s law is used. Mathematically, this form of the Raoult’s law is stated as: ptotal = p1°x1 + p2°x2 . Solutions which obey Raoult’s law over the entire range of concentration are called ideal solutions. Two types of deviations from Raoult’s law, called positive and negative deviations are observed. Azeotropes arise due to very large deviations from Raoult’s law.
The properties of solutions which depend on the number of solute particles and are independent of their chemical identity are called colligative properties. These are lowering of vapour pressure, elevation of boiling point, depression of freezing point and osmotic pressure. The process of osmosis can be reversed if a pressure higher than the osmotic pressure is applied to the solution. Colligative properties have been used to determine the molar mass of solutes. Solutes which dissociate in solution exhibit molar mass lower than the actual molar mass and those which associate show higher molar mass than their actual values.
Quantitatively, the extent to which a solute is dissociated or associated can be expressed by van’t Hoff factor i. This factor has been defined as ratio of normal molar mass to experimentally determined molar mass or as the ratio of observed colligative property to the calculated colligative property.
Exercises
2.1 Define the term solution. How many types of solutions are formed? Write briefly about each type with an example.
2.2 Give an example of a solid solution in which the solute is a gas.
2.3 Define the following terms:
(i) Mole fraction
(ii) Molality
(iii) Molarity
(iv) Mass percentage.
2.4 Concentrated nitric acid used in laboratory work is 68% nitric acid by mass in aqueous solution. What should be the molarity of such a sample of the acid if
the density of the solution is 1.504 g mL–1?
2.5 A solution of glucose in water is labelled as 10% w/w, what would be the molality and mole fraction of each component in the solution? If the density of
solution is 1.2 g mL–1, then what shall be the molarity of the solution?
2.6 How many mL of 0.1 M HCl are required to react completely with 1 g mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both?
2.7 A solution is obtained by mixing 300 g of 25% solution and 400 g of 40% solution by mass. Calculate the mass percentage of the resulting solution. 2.8 An antifreeze solution is prepared from 222.6 g of ethylene glycol (C2H6O2) and 200 g of water. Calculate the molality of the solution. If the density of the solution is 1.072 g mL–1, then what shall be the molarity of the solution?
2.9 A sample of drinking water was found to be severely contaminated with chloroform (CHCl3) supposed to be a carcinogen. The level of contamination
was 15 ppm (by mass):
(i) express this in percent by mass
(ii) determine the molality of chloroform in the water sample.
2.10 What role does the molecular interaction play in a solution of alcohol and water?
2.11 Why do gases always tend to be less soluble in liquids as the temperature is raised?
2.12 State Henry’s law and mention some important applications?
2.13 The partial pressure of ethane over a solution containing 6.56 × 10–3 g of ethane is 1 bar. If the solution contains 5.00 × 10–2 g of ethane, then what shall be the partial pressure of the gas?
2.14 What is meant by positive and negative deviations from Raoult’s law and how is the sign of ΔmixH related to positive and negative deviations from Raoult’s law?
2.15 An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
2.16 Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will
be the vapour pressure of a mixture of 26.0 g of heptane and 35 g of octane?
2.17 The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molal solution of a non-volatile solute in it.
2.18 Calculate the mass of a non-volatile solute (molar mass 40 g mol–1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
2.19 A solution containing 30 g of non-volatile solute exactly in 90 g of water has a vapour pressure of 2.8 kPa at 298 K. Further, 18 g of water is then added to
the solution and the new vapour pressure becomes 2.9 kPa at 298 K. Calculate:
(i) molar mass of the solute
(ii) vapour pressure of water at 298 K.
2.20 A 5% solution (by mass) of cane sugar in water has freezing point of 271K. Calculate the freezing point of 5% glucose in water if freezing point of pure
water is 273.15 K.
2.21 Two elements A and B form compounds having formula AB2 and AB4. When dissolved in 20 g of benzene (C6H6), 1 g of AB2 lowers the freezing point by 2.3 K whereas 1.0 g of AB4 lowers it by 1.3 K. The molar depression constant for benzene is 5.1 K kg mol–1. Calculate atomic masses of A and B.
2.22 At 300 K, 36 g of glucose present in a litre of its solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of the solution is 1.52 bars at the same temperature, what would be its concentration?
2.23 Suggest the most important type of intermolecular attractive interaction in the following pairs.
(i)n-hexane and n-octane
(ii)I2 and CCl4
(iii)NaClO4 and water
(iv)methanol and acetone
(v)acetonitrile (CH3CN) and acetone (C3H6O).
2.24 Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain. Cyclohexane, KCl, CH3OH, CH3CN.
2.25 Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
(i) phenol
(ii) toluene
(iii) formic acid
(iv) ethylene glycol
(v) chloroform
(vi) pentanol.
2.26 If the density of some lake water is 1.25g mL–1 and contains 92 g of Na+ ions per kg of water, calculate the molality of Na+ ions in the lake.
2.27 If the solubility product of CuS is 6 × 10–16, calculate the maximum molarity of CuS in aqueous solution.
2.28 Calculate the mass percentage of aspirin (C9H8O4) in acetonitrile (CH3CN) when 6.5 g of C9H8O4 is dissolved in 450 g of CH3CN.
2.29 Nalorphene (C19H21NO3), similar to morphine, is used to combat withdrawal symptoms in narcotic users. Dose of nalorphene generally given is 1.5 mg. Calculate the mass of 1.5 – 10–3 m aqueous solution required for the above dose.
2.30 Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 mL of 0.15 M solution in methanol.
2.31 The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroacetic acid increases in the order given above. Explain briefly.
2.32 Calculate the depression in the freezing point of water when 10 g of CH3CH2CHClCOOH is added to 250 g of water. Ka = 1.4 × 10 –3, Kf = 1.86 K kg mol–1.
2.33 19.5 g of CH2FCOOH is dissolved in 500 g of water. The depression in the freezing point of water observed is 1.00° C. Calculate the van’t Hoff factor and dissociation constant of fluoroacetic acid.
2.34 Vapour pressure of water at 293 K is 17.535 mm Hg. Calculate the vapour pressure of water at 293 K when 25 g of glucose is dissolved in 450 g of water.
2.35 Henry’s law constant for the molality of methane in benzene at 298 K is 4.27 × 105 mm Hg. Calculate the solubility of methane in benzene at 298 K under 760 mm Hg.
2.36 100 g of liquid A (molar mass 140 g mol–1) was dissolved in 1000 g of liquid B (molar mass 180 g mol–1). The vapour pressure of pure liquid B was found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 Torr.
2.37 Vapour pressures of pure acetone and chloroform at 328 K are 741.8 mm Hg and 632.8 mm Hg respectively. Assuming that they form ideal solution over the entire range of composition, plot p total, p chloroform, and p acetone as a function of xacetone. The experimental data observed for different compositions of mixture is:
| 100 × xacetone | 0 | 11.8 | 23.4 | 36.0 | 50.8 | 58.2 | 64.5 | 72.1 |
|---|---|---|---|---|---|---|---|---|
| Pacetone/mm Hg | 0 | 54.9 | 110.1 | 202.4 | 322.7 | 405.9 | 454.1 | 521.1 |
| Pchloroform /mm Hg | 632.8 | 548.1 | 469.4 | 359.7 | 257.7 | 193.6 | 161.2 | 120.7 |
Plot this data also on the same graph paper. Indicate whether it has positive deviation or negative deviation from the ideal solution.
2.38 Benzene and toluene form ideal solution over the entire range of composition. The vapour pressure of pure benzene and naphthalene at 300 K are 50.71 mm Hg and 32.06 mm Hg respectively. Calculate the mole fraction of benzene in vapour phase if 80 g of benzene is mixed with 100 g of naphthalene.
2.39 The air is a mixture of a number of gases. The major components are oxygen and nitrogen with approximate proportion of 20% is to 79% by volume at 298 K. The water is in equilibrium with air at a pressure of 10 atm. At 298 K if the Henry’s law constants for oxygen and nitrogen at 298 K are 3.30 × 107 mm and 6.51 × 107 mm respectively, calculate the composition of these gases in water.
2.40 Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 27° C.
2.41 Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 litre of water at 25° C, assuming that it is completely dissociated.
Answers to Some Intext Questions
2.1 C6H6 = 15.28%, CCl4 = 84.72%
2.2 0.459, 0.541
2.3 0.024 M, 0.03 M
2.4 37.5 g
2.5 1.5 mol kg–1 , 1.45 mol L–1 0.0263
2.9 289.5 bar
2.10 1.86 g
2.11 xA = 0.4, yA = 0.3; xB = 0.6, yB = 0.7
2.12 23.4 mm Hg, 0.017
I. Multiple Choice Questions (Type-I)
1. Which of the following units is useful in relating concentration of solution with its vapour pressure?
(i) mole fraction
(ii) parts per million
(iii) mass percentage
(iv) molality
2. On dissolving sugar in water at room temperature solution feels cool to touch. Under which of the following cases dissolution of sugar will be most rapid?
(i) Sugar crystals in cold water.
(ii) Sugar crystals in hot water.
(iii) Powdered sugar in cold water.
(iv) Powdered sugar in hot water.
3. At equilibrium the rate of dissolution of a solid solute in a volatile liquid solvent is __________.
(i) less than the rate of crystallisation
(ii) greater than the rate of crystallisation
(iii) equal to the rate of crystallisation
(iv) zero
4. A beaker contains a solution of substance ‘A’. Precipitation of substance ‘A’ takes place when small amount of ‘A’ is added to the solution. The solution is _________.
(i) saturated
(ii) supersaturated
(iii) unsaturated
(iv) concentrated
5. Maximum amount of a solid solute that can be dissolved in a specified amount of a given liquid solvent does not depend upon ____________.
(i) Temperature
(ii) Nature of solute
(iii) Pressure
(iv) Nature of solvent
6. Low concentration of oxygen in the blood and tissues of people living at high altitude is due to ____________.
(i) low temperature
(ii) low atmospheric pressure
(iii) high atmospheric pressure
(iv) both low temperature and high atmospheric pressure
7. Considering the formation, breaking and strength of hydrogen bond, predict which of the following mixtures will show a positive deviation from Raoult’s law?
(i) Methanol and acetone.
(ii) Chloroform and acetone.
(iii) Nitric acid and water.
(iv) Phenol and aniline.
8. Colligative properties depend on ____________.
(i) the nature of the solute particles dissolved in solution.
(ii) the number of solute particles in solution.
(iii) the physical properties of the solute particles dissolved in solution.
(iv) the nature of solvent particles.
9. Which of the following aqueous solutions should have the highest boiling point?
(i) 1.0 M NaOH
(ii) 1.0 M Na2SO4
(iii) 1.0 M NH4NO3
(iv) 1.0 M KNO3
10. The unit of ebulioscopic constant is _______________.
(i) K kg mol–1 or K (molality)–1
(ii) mol kg K–1 or K–1(molality)
(iii) kg mol–1 K–1 or K–1(molality)–1
(iv) K mol kg–1 or K (molality)
11. In comparison to a 0.01 M solution of glucose, the depression in freezing point of a 0.01 M MgCl2 solution is _____________.
(i) the same
(ii) about twice
(iii) about three times
(iv) about six times
12. An unripe mango placed in a concentrated salt solution to prepare pickle, shrivels because _____________.
(i) it gains water due to osmosis.
(ii) it loses water due to reverse osmosis.
(iii) it gains water due to reverse osmosis.
(iv) it loses water due to osmosis.
13. At a given temperature, osmotic pressure of a concentrated solution of a substance _____________.
(i) is higher than that at a dilute solution.
(ii) is lower than that of a dilute solution.
(iii) is same as that of a dilute solution.
(iv) cannot be compared with osmotic pressure of dilute solution.
14. Which of the following statements is false?
(i) Two different solutions of sucrose of same molality prepared in different solvents will have the same depression in freezing point.
(ii) The osmotic pressure of a solution is given by the equation Π = CRT ( where C is the molarity of the solution).
(iii) Decreasing order of osmotic pressure for 0.01 M aqueous solutions of barium chloride, potassium chloride, acetic acid and sucrose is BaCl2 > KCl > CH3COOH > sucrose.
(iv) According to Raoult’s law, the vapour pressure exerted by a volatile component of a solution is directly proportional to its mole fraction in the solution.
15. The values of Van’t Hoff factors for KCl, NaCl and K2SO4, respectively, are _____________.
(i) 2, 2 and 2
(ii) 2, 2 and 3
(iii) 1, 1 and 2
(iv) 1, 1 and 1
16. Which of the following statements is false?
(i) Units of atmospheric pressure and osmotic pressure are the same.
(ii) In reverse osmosis, solvent molecules move through a semipermeable membrane from a region of lower concentration of solute to a region of higher concentration.
(iii) The value of molal depression constant depends on nature of solvent.
(iv) Relative lowering of vapour pressure, is a dimensionless quantity.
17. Value of Henry’s constant KH ____________.
(i) increases with increase in temperature.
(ii) decreases with increase in temperature.
(iii) remains constant.
(iv) first increases then decreases.
18. The value of Henry’s constant KH is _____________.
(i) greater for gases with higher solubility.
(ii) greater for gases with lower solubility.
(iii) constant for all gases.
(iv) not related to the solubility of gases.
19. Consider the Fig. 2.1 and mark the correct option.
–
(i) water will move from side (A) to side (B) if a pressure lower than osmotic pressure is applied on piston (B).
(ii) water will move from side (B) to side (A) if a pressure greater than osmotic pressure is applied on piston (B).
(iii) water will move from side (B) to side (A) if a pressure equal to osmotic pressure is applied on piston (B).
(iv) water will move from side (A) to side (B) if pressure equal to osmotic pressure is applied on piston (A).
20. We have three aqueous solutions of NaCl labelled as ‘A’, ‘B’ and ‘C’ with concentrations 0.1M, 0.01M and 0.001M, respectively. The value of van’t Hoff factor for these solutions will be in the order______.
(i) iA< iB< iC
(ii) iA> iB> iC
(iii) iA= iB= iC
(iv) iA< iB> iC
21. On the basis of information given below mark the correct option.
Information:
(A) In bromoethane and chloroethane mixture intermolecular interactions of A–A and B–B type are nearly same as A–B type interactions.
(B) In ethanol and acetone mixture A–A or B–B type intermolecular interactions are stronger than A–B type interactions.
(C) In chloroform and acetone mixture A–A or B–B type intermolecular interactions are weaker than A–B type interactions.
(i) Solution (B) and (C) will follow Raoult’s law.
(ii) Solution (A) will follow Raoult’s law.
(iii) Solution (B) will show negative deviation from Raoult’s law.
(iv) Solution (C) will show positive deviation from Raoult’s law.
22. Two beakers of capacity 500 mL were taken. One of these beakers, labelled as “A”, was filled with 400 mL water whereas the beaker labelled “B” was filled with 400 mL of 2 M solution of NaCl. At the same temperature both the beakers were placed in closed containers of same material and same capacity as shown in Fig. 2.2.
–
At a given temperature, which of the following statement is correct about the vapour pressure of pure water and that of NaCl solution.
(i) vapour pressure in container (A) is more than that in container (B).
(ii) vapour pressure in container (A) is less than that in container (B).
(iii) vapour pressure is equal in both the containers.
(iv) vapour pressure in container (B) is twice the vapour pressure in container (A).
23. If two liquids A and B form minimum boiling azeotrope at some specific composition then _______________.
(i) A–B interactions are stronger than those between A–A or B–B.
(ii) vapour pressure of solution increases because more number of molecules of liquids A and B can escape from the solution.
(iii) vapour pressure of solution decreases because less number of molecules of only one of the liquids escape from the solution.
(iv) A–B interactions are weaker than those between A–A or B–B.
24. 4L of 0.02 M aqueous solution of NaCl was diluted by adding one litre of water. The molality of the resultant solution is _____________.
(i) 0.004
(ii) 0.008
(iii) 0.012
(iv) 0.016
25. On the basis of information given below mark the correct option.
Information : On adding acetone to methanol some of the hydrogen bonds between methanol molecules break.
(i) At specific composition methanol-acetone mixture will form minimum boiling azeotrope and will show positive deviation from Raoult’s law.
(ii) At specific composition methanol-acetone mixture forms maximum boiling azeotrope and will show positive deviation from Raoult’s law.
(iii) At specific composition methanol-acetone mixture will form minimum boiling azeotrope and will show negative deviation from Raoult’s law.
(iv) At specific composition methanol-acetone mixture will form maximum boiling azeotrope and will show negative deviation from Raoult’s law.
26. KH value for Ar(g), CO2(g), HCHO (g) and CH4(g) are 40.39, 1.67, 1.83 x 10–5 and 0.413 respectively.
Arrange these gases in the order of their increasing solubility.
(i) HCHO < CH4 < CO2 < Ar
(ii) HCHO < CO2 < CH4 < Ar
(iii) Ar < CO2 < CH4 < HCHO
(iv) Ar < CH4 < CO2 < HCHO
II. Multiple Choice Questions (Type-II)
Note : In the following questions two or more options may be correct.
27. Which of the following factor (s) affect the solubility of a gaseous solute in the fixed volume of liquid solvent?
(a) nature of solute (b) temperature (c) pressure
(i) (a) and (c) at constant T
(ii) (a) and (b) at constant P
(iii) (b) and (c) only
(iv) (c) only
28. Intermolecular forces between two benzene molecules are nearly of same strength as those between two toluene molecules. For a mixture of benzene and toluene, which of the following are not true?
(i) ΔmixH = zero
(ii) ΔmixV = zero
(iii) These will form minimum boiling azeotrope.
(iv) These will not form ideal solution.
29. Relative lowering of vapour pressure is a colligative property because _____________.
(i) It depends on the concentration of a non electrolyte solute in solution and does not depend on the nature of the solute molecules.
(ii) It depends on number of particles of electrolyte solute in solution and does not depend on the nature of the solute particles.
(iii) It depends on the concentration of a non electrolyte solute in solution as well as on the nature of the solute molecules.
(iv) It depends on the concentration of an electrolyte or nonelectrolyte solute in solution as well as on the nature of solute molecules.
30. Van’t Hoff factor i is given by the expression _____________.
(i) i = Normal molar mass/Abnormalmolar mass
(ii) i= Abnormal molar mass/Normal molar mass
(iii) i = Observed colligative property/Calculated colligative property
(iv) i= Calculated colligative property/Observed colligative property
31. Isotonic solutions must have the same _____________.
(i) solute
(ii) density
(iii) elevation in boiling point
(iv) depression in freezing point
32. Which of the following binary mixtures will have same composition in liquid and vapour phase?
(i) Benzene – Toluene
(ii) Water-Nitric acid
(iii) Water-Ethanol
(iv) n-Hexane – n-Heptane
33. In isotonic solutions ________________.
(i) solute and solvent both are same.
(ii) osmotic pressure is same.
(iii) solute and solvent may or may not be same.
(iv) solute is always same solvent may be different.
34. For a binary ideal liquid solution, the variation in total vapour pressure versus composition of solution is given by which of the curves?
–
35. Colligative properties are observed when _____________.
(i) a non volatile solid is dissolved in a volatile liquid.
(ii) a non volatile liquid is dissolved in another volatile liquid.
(iii) a gas is dissolved in non volatile liquid.
(iv) a volatile liquid is dissolved in another volatile liquid.
III. Short Answer Type
36. Components of a binary mixture of two liquids A and B were being separated by distillation. After some time separation of components stopped and composition of vapour phase became same as that of liquid phase. Both the components started coming in the distillate. Explain why this happened.
37. Explain why on addition of 1 mol of NaCl to 1 litre of water, the boiling point of water increases, while addition of 1 mol of methyl alcohol to one litre of water decreases its boiling point.
38. Explain the solubility rule “like dissolves like” in terms of intermolecular forces that exist in solutions.
39. Concentration terms such as mass percentage, ppm, mole fraction and molality are independent of temperature, however molarity is a function of temperature.
Explain.
40. What is the significance of Henry’s Law constant KH?
41. Why are aquatic species more comfortable in cold water in comparison to warm water?
42. (a) Explain the following phenomena with the help of Henry’s law.
(i) Painful condition known as bends.
(ii) Feeling of weakness and discomfort in breathing at high altitude.
(b) Why soda water bottle kept at room temperature fizzes on opening?
43. Why is the vapour pressure of an aqueous solution of glucose lower than that of water?
44. How does sprinkling of salt help in clearing the snow covered roads in hilly areas? Explain the phenomenon involved in the process.
45. What is “semi permeable membrane”?
46. Give an example of a material used for making semipermeable membrane for carrying out reverse osmosis.
IV. Matching Type
Note : In the following questions match the items given in Column I and Column II.
47. Match the items given in Column I and Column II.
| Column I | Column II | ||
| (i) | Saturated solution | (a) | Solution having same osmotic pressure at a given temperature as that of given solution. |
| (ii) | Binary solution | (b) | A solution whose osmotic pressure is less than that of another. |
| (iii) | Isotonic solution | (c) | Solution with two components. |
| (iv) | Hypotonic solution | (d) | A solution which contains maximum amount of solute that can be dissolved in a given amount of solvent at a given temperature. |
| (v) | Solid solution | (e) | A solution whose osmotic pressure is more than that of another. |
| (vi) | Hypertonic solution | (f) | A solution in solid phase. |
48. Match the items given in Column I with the type of solutions given in Column II.
| Column I | Column II | ||
| (i) | Soda water | (a) | A solution of gas in solid |
| (ii) | Sugar solution | (b) | A solution of gas in gas |
| (iii) | German silver | (c) | A solution of solid in liquid |
| (iv) | Air | (d) | A solution of solid in solid |
| (v) | Hydrogen gas in palladium | (e) | A solution of gas in liquid |
| (f) | A solution of liquid in solid |
49. Match the laws given in Column I with expresions given in Column II.
| Column I | Column II | ||
| (i) | Raoult’s law | (a) | ΔTf = Kfm |
| (ii) | Henry’s law | (b) | Π = CRT |
| (iii) | Elevation of boiling point | (c) | p = x1p1o + x2p2o |
| (iv) | Depression in freezing point | (d) | ΔTb = Kbm |
| (v) | Osmotic pressure | (e) | p = KH.x |
50. Match the terms given in Column I with expressions given in Column II.
| Column I | Column II | ||
| (i) | Mass percentage | (a) | Number of moles of the solute component Volume of solution in litres |
| (ii) | Volume percentage | (b) | Number of moles of a component / Total number of moles of all the components |
| (iii) | Mole fraction | (c) | Volume of the solute component in solution x 100 / Total volume of solution |
| (iv) | Molality | (d) | Mass of the solute component in solution x 100/Total mass of the solution |
| (v) | Molarity | (e) | Number of moles of the solute components/Mass of solvent in kilograms |
V. Assertion and Reason Type
Note : In the following questions a statement of assertion followed by a statement of reason is given. Choose the correct answer out of the following
choices.
(i) Assertion and reason both are correct statements and reason is correct explanation for assertion.
(ii) Assertion and reason both are correct statements but reason is not correct explanation for assertion.
(iii) Assertion is correct statement but reason is wrong statement.
(iv) Assertion and reason both are incorrect statements.
(v) Assertion is wrong statement but reason is correct statement.
51. Assertion : Molarity of a solution in liquid state changes with temperature.
Reason : The volume of a solution changes with change in temperature.
52. Assertion : When methyl alcohol is added to water, boiling point of water increases.
Reason : When a volatile solute is added to a volatile solvent elevation in boiling point is observed.
53. Assertion : When NaCl is added to water a depression in freezing point is observed.
Reason : The lowering of vapour pressure of a solution causes depression in the freezing point.
54. Assertion : When a solution is separated from the pure solvent by a semipermeable membrane, the solvent molecules pass through it from pure solvent side to the solution side.
Reason : Diffusion of solvent occurs from a region of high concentration solution to a region of low concentration solution.
VI. Long Answer Type
55. Define the following modes of expressing the concentration of a solution. Which of these modes are independent of temperature and why?
(i) w/w (mass percentage) (v) x (mole fraction)
(ii) V/V (volume percentage) (vi) M (Molarity)
(iii) w/V (mass by volume percentage) (vii) m (Molality)
(iv) ppm. (parts per million)
56. Using Raoult’s law explain how the total vapour pressure over the solution is related to mole fraction of components in the following solutions.
(i) CHCl2 (l) and CH2Cl2(l) (ii) NaCl(s) and H2O (l)
57. Explain the terms ideal and non-ideal solutions in the light of forces of interactions operating between molecules in liquid solutions.
58. Why is it not possible to obtain pure ethanol by fractional distillation? What general name is given to binary mixtures which show deviation from Raoult’s law and whose components cannot be separated by fractional distillation. How many types of such mixtures are there?
59. When kept in water, raisin swells in size. Name and explain the phenomenon involved with the help of a diagram. Give three applications of the phenomenon.
60. Discuss biological and industrial importance of osmosis.
61. How can you remove the hard calcium carbonate layer of the egg without damaging its semiprermiable membrane? Can this egg be inserted into a bottle with a narrow neck without distorting its shape? Explain the process involved.
62. Why is the mass determined by measuring a colligative property in case of some solutes abnormal ? Discuss it with the help of Van’t Hoff factor.
ANSWERS
I. Multiple Choice Questions (Type-I)
1. (i) 2. (iv) 3. (iii)
4. (ii), [Hint : If added substance dissolves, the solution is unsaturated. If it does not dissolve solution is saturated. If precipitation occurs solution
is supersaturated.]
5. (iii)
6. (ii), [Hint : Body temperature of human beings remains constant.]
7. (i) 8. (ii) 9. (ii) 10. (i) 11. (iii) 12. (iv) 13. (i) 14. (i) 15. (ii) 16. (ii) 17. (i) 18. (ii) 19. (ii) 20. (iii) 21. (ii) 22. (i) 23. (i) 24. (iv) 25. (ii) 26. (iii)
II. Multiple Choice Questions (Type-II)
27. (i), (ii) 28. (iii), (iv) 29. (i), (ii) 30. (i), (iii) 31. (ii), (iii) 32. (ii), (iii) 33. (ii), (iii) 34. (i), (iv) 35. (i), (ii)
III. Short Answer Type
36. Since both the components are appearing in the distillate and composition of liquid and vapour is same, this shows that liquids have formed azeotropic mixture and hence cannot be separated at this stage by distillation.
37. NaCl is a non volatile solute, therefore, addition of NaCl to water lowers the vapour pressure of water. As a result boiling point of water increases. Methyl alcohol on the other hand is more volatile than water, therefore its addition increases, the total vapour pressure over the solution and a decrease in boiling point of water results.
38. A substance (solute) dissolves in a solvent if the intermolecular interactions are similar in both the components; for example, polar solutes dissolve in polar solvents and non polar solutes in non polar solvents thus we can say “like dissolves like”.
39. Molarity of a solution is defined as the number of moles of solute dissolved in one litre of solution. Since volume depends on temperature and undergoes a change with change in temperature, the molarity will also change with change in temperature. On the other hand, mass does not change with change in temperature, as a result other concentration terms given in the question remain unchanged by changing temperature. According to the definition of all these terms, mass of the solvent used for making the solution is related to the mass of solute.
40. Higher the value of Henry’s law constant KH, the lower is the solubility of the gas in the liquid.
41. At a given pressure the solubility of oxygen in water increases with decrease in temperature. Presence of more oxygen at lower temperature makes the aquatic species more comfortable in cold water.
42. Refer to the NCERT textbook for Class XII.
43. In pure liquid water the entire surface of liquid is occupied by the molecules of water. When a non volatile solute, for example glucose is dissolved in water, the fraction of surface covered by the solvent molecules gets reduced because some positions are occupied by glucose molecules. As a result number of solvent molecules escaping from the surface also gets reduced, consequently the vapour pressure of aqueous solution of glucose is reduced.
44. When salt is spread over snow covered roads, snow starts melting from the surface because of the depression in freezing point of water and it helps in clearing the roads.
45. Continuous sheets or films (natural or synthetic) which contain a network of submicroscopic holes or pores through which small solvent molecules like water can pass; but the passage of bigger molecules of solute is hindered, are known as semi permeable membrane.
46. Cellulose acetate.
IV. Matching Type
47. (i) → (d) (ii) → (c) (iii) → (a) (iv) → (b) (v) → (f) (vi) → (e)
48. (i) → (e) (ii) → (c) (iii) → (d) (iv) → (b) (v) → (a)
49. (i) → (c) (ii) → (e) (iii) → (d) (iv) → (a) (v) → (b)
50. (i) → (d) (ii) → (c) (iii) → (b) (iv) → (e) (v) → (a)
V. Assertion and Reason Type
51. (i) 52. (iv) 53. (i) 54. (ii)
VI. Long Answer Type
55. Refer to NCERT textbook for Class XII.
56. Hint : Discuss the following formulas
(i) for a binary solution having both components as volatile liquids, the total pressure will be
p = p1 = x1p10 + x2p20
= x1p10 + (1–x1)p20
= (p10 – p20 ) x1+ p20
p = total vapour pressure
p1 = partial vapour pressure of component 1
p2 = partial vapour pressure of component 2.
(ii) For a solution containing non-volatile solute, the Raoult’s law is applicable only to vaporisable component (1) and total vapour pressure is written as
p = p1 = x1p10
57. Refer to page 45 of NCERT textbook for Class XII.
58. See page 46 of NCERT textbook for Class XII.
59. [Hint : Explain it with the help of a diagram (Fig. 2.3) illustrating the osmosis of water into raisin.]
–
60. Hint : The process of osmosis is of immense biological and industrial importance as is evident from the following examples :
(i) Movement of water from soil into plant roots and subsequently into upper portion of the plant is partly due to osmosis.
(ii) Preservation of meat against bacterial action by adding salt.
(iii) Preservation of fruits against bacterial action by adding sugar. Bacterium in canned fruit loses water through the process of osmosis, shrivels and dies.
(iv) Reverse osmosis is used for desalination of water.
61. Hint :
–
62. Certain compounds when dissolved in suitable solvents either dissociate or associate.
For example ethanoic acid dimerises in benzene due to hydrogen bonding, while in water, it dissociates and forms ions. As a result the number of chemical species in solution increases or decreases as compared to the number of chemical species of solute added to form the solution. Since the magnitude of colligative property depends on the number of solute particles, it is expected that the molar mass determined on the basis of colligative properties will be either higher or lower than the expected value or the normal value and is called abnormal molar mass.
In order to account for the extent of dissociation or association of molecules in solution, Van’t Hoff introduced a factor, i, known as the Van’t Hoff factor. It can be defined as follows.
i = Expected molar mass/Abnormalmolar mass
= Observed colligative property/Calculated colligative property
= (Total number of moles of particles after association/dissociation)/(Number of moles of particles before association/dissociation)
xxxxxxxxxxxxxxxxxxxxxx
Simplified Knowledge Management Classes
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
Do you want to make money working at home ?
see http://skmclasses.weebly.com/jobs.html
–
search for videos in http://www.skmclasses.weebly.com
you will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
http://skmclasses.wordpress.com/accolades-and-appreciations-received-from-students-and-parents/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
http://skmclasses4olympiads.wordpress.com/
https://skmclasses.wordpress.com/cbse-standard-12-chemistry-polymers-chapter-15-ncert/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
https://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://iitjee.wix.com/skmclasses
http://skmclasses.wordpress.com/circular-motion-problems-for-iit-jee-cbse-from-skm-classes/
http://skmclasses4olympiads.wordpress.com/
http://skmclasses.wordpress.com/combinatorics-permutation-combination-for-iit-jee-cbse/
https://zookeepersblog.wordpress.com/iit-jee-capacitance/
https://zookeepersblog.wordpress.com/iit-jee-3d-geometry-solutions/
https://zookeepersblog.wordpress.com/iit-jee-algebra/
https://zookeepersblog.wordpress.com/iit-jee-area-problems/
https://zookeepersblog.wordpress.com/iit-jee-binomial-theorem/
https://zookeepersblog.wordpress.com/iit-jee-calculus/
https://zookeepersblog.wordpress.com/iit-jee-optics/
https://zookeepersblog.wordpress.com/iit-jee-co-ordinate-geometry/
https://zookeepersblog.wordpress.com/iit-jee-complex-number/
https://zookeepersblog.wordpress.com/iit-jee-current-electricity-circuits/
https://zookeepersblog.wordpress.com/iit-jee-determinant-and-matrices/
https://zookeepersblog.wordpress.com/iit-jee-differentiability/
https://zookeepersblog.wordpress.com/iit-jee-electromagnetics/
https://zookeepersblog.wordpress.com/iit-jee-electrostatics/
xxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxx
The following Videos are available for you ( As of Now ). These explain tricky Physics and Mathematics Numericals.
Eventually I will try to give Videos for full course here for you.
These covers PU ( Pre University courses, school / college ) courses, IIT JEE, AIEEE ( All India Engineering Entrance Examination ) , CET ( Combined Engineering Test ), AIPMT ( All India Pre Medical Test ), ISc ( Intermediate Science / Indian School Certificate Exam ), CBSE ( Central Board Secondary Exam ), Roorkey Joint Entrance Test Questions ( Discontinued since 2002 ), APhO ( Asian Physics Olympiad ), IPhO ( International Physics Olympiad ), IMO ( International Mathematics Olympiad ) , NSEP ( National Standard Exam in Physics ), RMO ( Regional Math Olympiad , India ), INMO ( Indian National Maths Olympiad ), Irodov Solutions, Prof. H C Verma ( Concepts of Physics ) Solutions etc.
( You can see the history of Indian Participation in various Olympiads at -> https://zookeepersblog.wordpress.com/indian-participation-in-ipho-icho-ibo-and-astronomy-olympiad/ )
[ In each of these videos there is at-least 1 or more errors. Please tell me about those ]
Simplified Knowledge Management Classes
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
Do you want to make money working at home ?
see http://skmclasses.weebly.com/jobs.html
–
search for videos in http://www.skmclasses.weebly.com
you will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
http://skmclasses.wordpress.com/accolades-and-appreciations-received-from-students-and-parents/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
http://skmclasses4olympiads.wordpress.com/
https://skmclasses.wordpress.com/cbse-standard-12-chemistry-polymers-chapter-15-ncert/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
https://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://iitjee.wix.com/skmclasses
http://skmclasses.wordpress.com/circular-motion-problems-for-iit-jee-cbse-from-skm-classes/
http://skmclasses4olympiads.wordpress.com/
http://skmclasses.wordpress.com/combinatorics-permutation-combination-for-iit-jee-cbse/
Thanks and Regards
Zookeeper ;-D Subhashish Chattopadhyay
[ I suggest you see the videos starting with 1- first then starting with 2- ….. in that sequence. ]
[ Tell your friends about this link if you liked the videos ]
In case of doubts or suggestions, Please send me email at mokshya@gmail.com
Simplified Knowledge Management Classes
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
Do you want to make money working at home ?
see http://skmclasses.weebly.com/jobs.html
–
search for videos in http://www.skmclasses.weebly.com
you will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
http://skmclasses.wordpress.com/accolades-and-appreciations-received-from-students-and-parents/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
http://skmclasses4olympiads.wordpress.com/
https://skmclasses.wordpress.com/cbse-standard-12-chemistry-polymers-chapter-15-ncert/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
https://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://iitjee.wix.com/skmclasses
http://skmclasses.wordpress.com/circular-motion-problems-for-iit-jee-cbse-from-skm-classes/
http://skmclasses4olympiads.wordpress.com/
http://skmclasses.wordpress.com/combinatorics-permutation-combination-for-iit-jee-cbse/
Answers to -> Frequently Asked Questions ( FAQ ) [ commonly asked intelligent Questions 🙂 ]
Simplified Knowledge Management Classes
Must see https://zookeepersblog.wordpress.com/some-points-which-i-wish-all-my-new-prospective-students-know/
🙂
Do you want to make money working at home ?
see http://skmclasses.weebly.com/jobs.html
–
search for videos in http://www.skmclasses.weebly.com
you will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
http://skmclasses.wordpress.com/accolades-and-appreciations-received-from-students-and-parents/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
http://skmclasses4olympiads.wordpress.com/
https://skmclasses.wordpress.com/cbse-standard-12-chemistry-polymers-chapter-15-ncert/
http://skmclasses4olympiads.wordpress.com/
http://iitjee.wix.com/skmclasses
https://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://skmclasses.wordpress.com/complex-number-for-iit-jee-cbse-from-skm-classes-south-bangalore/
http://iitjee.wix.com/skmclasses
http://skmclasses.wordpress.com/circular-motion-problems-for-iit-jee-cbse-from-skm-classes/
http://skmclasses4olympiads.wordpress.com/
http://skmclasses.wordpress.com/combinatorics-permutation-combination-for-iit-jee-cbse/
xxxxxxxxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxxxx
The following Videos are available for you ( As of Now ). These explain tricky Physics and Mathematics Numericals.
Eventually I will try to give Videos for full course here for you.
These covers PU ( Pre University courses, school / college ) courses, IIT JEE, AIEEE ( All India Engineering Entrance Examination ) , CET ( Combined Engineering Test ), AIPMT ( All India Pre Medical Test ), ISc ( Intermediate Science / Indian School Certificate Exam ), CBSE ( Central Board Secondary Exam ), Roorkey Joint Entrance Test Questions ( Discontinued since 2002 ), APhO ( Asian Physics Olympiad ), IPhO ( International Physics Olympiad ), IMO ( International Mathematics Olympiad ) , NSEP ( National Standard Exam in Physics ), RMO ( Regional Math Olympiad , India ), INMO ( Indian National Maths Olympiad ), Irodov Solutions, Prof. H C Verma ( Concepts of Physics ) Solutions etc.
( You can see the history of Indian Participation in various Olympiads at ->
https://zookeepersblog.wordpress.com/indian-participation-in-ipho-icho-ibo-and-astronomy-olympiad/ )
[ In each of these videos there is at-least 1 or more errors. Please tell me about those ]
search for videos in http://www.skmclasses.weebly.com
You should get to see all the Uploaded videos. Though we have many more study videos.
Thanks and Regards
Zookeeper ;-D Subhashish Chattopadhyay
[ I suggest you see the videos starting with 1- first then starting with 2- ….. in that sequence. ]
[ Tell your friends about this link if you liked the videos ]
In case of doubts or suggestions, Please send me email at mokshya@gmail.com
search for videos in http://www.skmclasses.weebly.com
Answers to -> Frequently Asked Questions ( FAQ ) [ commonly asked intelligent Questions 🙂 ]
1 ) How do I prepare for IIT ?
Ans : – See the videos made by me ( search for videos in http://www.skmclasses.weebly.com
Though we have many more which have not been uploaded ). While watching the videos, take notes and try to solve the problems yourself by pausing the video. Tell me if any calculation is wrong. See the videos with 1- first then 2- and so on. Write to IAPT Kothrud, Pune office to buy ( 150 Rs approx ) the book with previous papers of NSEP ( National Standard Exam in Physics – The 1st level ), INPhO ( Indian National Physics Olympiad – 2nd level ). Prepare with these and see how much you are scoring. You can guess your ALL INDIA rank easily from NSEP, and INPhO rank. Since 1998 the IIT JEE toppers have been mostly representing India in IPhO.
2 ) Which codec and Player do I use to see the videos ?
Ans : – You can use GOM Player, or VLC Player. You have to have good speakers with filters or good earphones with filters. We have checked mostly it is OK with these. ( If you are depending only on your embedded speakers of computer /screen / keyboard then there may be extra distortions. As these speakers are often not of good Quality. Also install latest KL Codecs ) In any case reduce the volume see the board, imagine sitting in the last bench and solving the problems of your own. See if your solution differs anywhere with the scribbles on the board.
3 ) Why are you giving these ( high Quality ) lecture for free ?
Ans : Well there are lot of good things free in this world. Linux, My-SQL, Open-Office ….. Go to sourceforge and get thousands of high quality software free along with source code. Yes all officially free …. Why do you think Richard Stallman, Zimmerman, ….. etc are considered Guru philosophers ? In Punjab and Gurudwaras worldwide there are so many Langars where you get better food than Restaurants. ….. why ? Why do you have Dharmasalas and subsidized rest rooms near hospitals / Famous Temples / various places ? in Iftar party anyone can eat for free …. why ?
I am teaching since 1989 I have observed most students can do much better if they have the self motivation to solve and practice. Cheap books are available in second hand bookstalls, where you get thousands of Numericals to solve ….. but most students will like to blow their time going and coming for tuition, travel time …. TV for hours and hours watching cricket / Tennis games, playing computer games …. My free lectures are not going to make much difference in spending of unnecessary money for coaching ….. I know very well , how much people enjoy …. ! spending unnecessarily !!
–
Do you know that there are NO poor / needy students in Bangalore.
–
Sometime back I had tried to teach for IIT JEE FREE. Discussed with a few NGOs and social service guys. Arranged rooms but got only 1 student. We had informed many people in many ways to inform students …. We did not get students who are ready to learn for free. So I am sure these lectures are NOT FREE. If anyone learns from these, s/he changes and that’s the gain / benefit. This change ( due to learning ) is very costly …. Most do not want to learn ………..
search for videos in http://www.skmclasses.weebly.com
You will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
🙂
4 ) How can I get all your lectures ?
Ans : – Apart from my lectures there are approx 700 GB of PCM ( Phy, Chem, Math ) lectures. It takes approx 3 years of continuous download from scattered sources. I have ( 20,000 )Thousands of these. You can take ALL of them from me in an external 1 TB hard disk, instead of spending so much money and time again for downloading. These cover ( by Various Professors ) everything of Chemistry, Physics, Maths… Lot of this is from outside India … as foreigners have much wider heart than Indians ( as most of GNU / open source software have been developed by Non-Indians ). I observed the gaps in these videos, and thus I am solving IIT, APhO, Roorkey, IPhO Numericals. Videos made by me along with these videos gives a complete preparation.
Send me a mail at mokshya@gmail.com to contact me.
search for videos in http://www.skmclasses.weebly.com
You will get most videos. I say most because I do not upload all videos that I make. I have many more videos which are not in the net.
🙂
5 ) How do you get benefited out of this ?
Ans :- If anyone learns we all will have better people in this world. I will have better “ YOU “.
🙂
6 ) Why do you call yourself a Zookeeper ?
Ans :- This is very nicely explained at https://zookeepersblog.wordpress.com/z00keeper-why-do-i-call-myself-a-zoookeeper/
🙂
7 ) Where do you stay ?
Ans :- Presently I am in Bangalore.
🙂
8 ) If I need videos in a few topics can you make them for me ?
Ans :- We actively answers doubts at doubtpoint.
see http://skmclasses.weebly.com/doubtpoint.html
In case you appreciate our time and efforts involved in answering complicated Questions, then get Quality answers at doubtpoint.
🙂
9 ) Why did you write an article saying there are No Poor students ?
Ans :- There are lots of NGOs and others working for rural / poor children education at lower classes. While very less effort is on for std 9 till 12. Also see the answer in question number ( 3 ) above. In more than 2 decades of teaching I never met a Poor child who was seriously interested in ( higher ) studies. As I have a mind / thinking of a ” Physicist “, I go by ” Experimental Observation “.
It is not about what is being said about poor in media / TV etc, or ” what it should be ” ( ? ) …. It is about what I see happening. Also to add ( confuse ? you more )…. You must be knowing that in several states over many years now girl students have better ( by marks as well as by pass percentage ) result in std 10 / Board Exams….. well but NEVER a girl student came FIRST in IIT JEE … why ? [ The best rank by a Girl student is mostly in 2 digits, very rarely in single digit ] ????? So ????
🙂
10 ) How much do I have to study to make it to IIT ?
Ans :- My experience of Teaching for IIT JEE since 1989, tells me, Total 200 hours per subject ( PCM ) is sufficient. If you see my Maths and Physics videos, each subject is more than 200 hours. So if someone sees all the videos diligently, takes notes and remembers, …… Done.
🙂
11 ) What is EAMCET ?
Ans :- Engineering Agriculture and Medicine Common Entrance Test is conducted by JNT University Hyderabad on behalf of APSCHE. This examination is the gateway for entry into various professional courses offered in Government/Private Colleges in Andhra Pradesh.
12 ) In your videos are you covering other Exams apart from IIT ?
Ans : – Yes. See many videos made by solving problems of MPPET, Rajasthan / J&K CET, UPSEAT ( UPES Engineering Aptitude Test ), MHCET, BCECE ( Bihar Combined Entrance Competitive Examination Board ), WB JEE etc
🙂
13 ) What is SCRA ?
Ans : – Special Class Railway Apprentice (SCRA) exam is conducted by Union Public Service Commission (UPSC) board, for about 10 seats.That translates into an astonishing ratio of 1 selection per 10,000 applicants. The SCRA scheme was started in 1927 by the British, to select a handful of most intelligent Indians to assist them in their Railway Operations, after training at their Railway’s largest workshop, i.e. Jamalpur Workshop, and for one year in United Kingdom. The selected candidates were required to appear in the Mechanical Engineering Degree Examination held by Engineering Council (London).
Thanks for your time. To become my friend in google+ ( search me as mokshya@gmail.com and send friend request )
Read http://edge.org/responses/what-scientific-concept-would-improve-everybodys-cognitive-toolkit
🙂
The following video is a must see for full CO2 cycle, plates of Earth, Geological activities, stability of weather
http://www.youtube.com/watch?v=oIuoNtRBG4w
🙂
Article in Nature says CO2 increase is good for the trees
http://thegwpf.org/science-news/6086-co2-is-greening-the-planet-savannahs-soon-to-be-covered-by-forests.html
🙂
http://climaterealists.com/index.php?id=9752
BBC documentary Crescent and Cross shows the 1000 years of fight between Christians and Muslims. Millions have been killed in the name of Religion. To decided whose GOD is better, and which GOD to follow. The fight continues.
–
Summary of Women
http://www.youtube.com/watch?v=yIpmML49hMU
🙂
The Virus of Faith
http://www.youtube.com/watch?v=scarHc8RA0g
🙂
The God delusion
http://www.youtube.com/watch?v=LVr9bJ8Sctk
🙂
cassiopeia facts about evolution
http://www.youtube.com/watch?v=K7tQIB4UdiY
–
Intermediate Fossil records shown and explained nicely Fossils, Genes, and Embryos http://www.youtube.com/watch?v=fdpMrE7BdHQ
The Rise Of Narcissism In Women
http://www.youtube.com/watch?v=wZHKCbHGlS0
🙂
13 type of women whom you should never court
http://timesofindia.indiatimes.com/life-style/relationships/man-woman/13-Women-you-should-never-court/articleshow/14637014.cms
🙂
Media teaching Misandry in India
http://www.youtube.com/watch?v=-M2txSbOPIo
Summary of problems with women
http://problemwithwomentoday.blogspot.in/2009/12/problem-with-women-today-what-in-hell.html
🙂
Eyeopener men ? women only exists
http://www.youtube.com/watch?v=6ZAuqkqxk9A
🙂
Each of you is an Activist in some way or other. You are trying to propagate those thoughts, ideas that you feel concerned / excited about.
–
Did you analyze your effectiveness ?
http://www.youtube.com/watch?v=61qn7S9NCOs
Culturomics can help you
😀
see how biased women are. Experimental proof. Women are happy when they see another woman is beating a man ( see how women misbehave with men )
🙂
http://www.youtube.com/watch?v=LlFAd4YdQks
–
see detailed statistics at
http://www.youtube.com/watch?v=5lHmCN3MBMI
An eye opener in Misandry
http://www.youtube.com/watch?v=YiTaDS_X6CU
My sincere advice would be to be EXTREMELY careful ( and preferably away ) of girls. As girls age; statistically certain behavior in them has been observed. Most Male can NOT manage those behaviors… Domestic violence, divorce etc are rising very fast. Almost in all cases boys / males are HUGE loosers. Be extremely choosy ( and think from several angles ) before even talking to a girl.
🙂
https://zookeepersblog.wordpress.com/save-the-male/
🙂
How women manipulate men
http://www.angryharry.com/esWomenManipulateMen.htm
Gender Biased Laws in India
https://zookeepersblog.wordpress.com/biased-laws/
🙂
Only men are victimised
http://www.youtube.com/watch?v=4JA4EPRbWhQ
Men are BETTER than women
http://www.menarebetterthanwomen.com/
🙂
see http://www.youtube.com/watch?&v=T0xoKiH8JJM#!
🙂
Male Psychology http://www.youtube.com/watch?v=uwxgavf2xWE
Women are more violent than men
http://www.independent.co.uk/news/uk/home-news/women-are-more-violent-says-study-622388.html
🙂
In the year 2010, 168 men ended their lives everyday ( on average ). More husbands committed suicide than wives.
🙂
http://www.rediff.com/news/report/ncrb-stats-show-more-married-men-committing-suicide/20111028.htm
It is EXTREMELY unfortunate that media projects men as fools, women as superiors, Husbands as servants, and replaceable morons. In ad after ad worldwide from so many companies, similar msg to disintegrate the world is being bombarded. It is highly unacceptable misandry
🙂
http://www.youtube.com/watch?v=oq14WHkFq30
It is NOT at all funny that media shows violence against MEN. Some advertisers are trying to create a new ” Socially acceptable culture ” of slapping Men ( by modern city women ). We ( all men ) take objection to these advertisements.
We oppose this Misandry bad culture. Please share to increase awareness against Men bashing
🙂
http://www.youtube.com/watch?v=D8ecN2rh0uU
Think what are you doing … why are you doing ?
http://www.youtube.com/watch?v=qp0HIF3SfI4
Every Man must know this …
http://www.youtube.com/watch?v=cIFmQHJEG1M
🙂
Manginas, White Knights, & Other Chivalrous Dogs
http://www.youtube.com/watch?v=oXQDtBT70B8
!
!
: ****__********__***
…….. (””(`-“’´´-´)””)
……….)…..–…….–….(
………/…..(6…_…6)….\
………\……..(..0..)….;../
……__.`.-._..’=’…_.-.`.__
…./……’###.,.–.,.###.’…\
….\__))####’#’###(((__/
……##### u r #####
……..### SWEET. ###
……/….#########…\
..__\…..\..######/…../
(.(.(____)….`.#.´..(____).).)
Visual Dictionary from SKMClasses for tough Vocabulary, in cartoon forms, for SAT, GRE, CAT, and other vital English exams
and
https://skmclasses.wordpress.com/accolades-and-appreciations-received-from-students-and-parents/
________________________________________________________
_________________________________________________________________________
IIT, JEE,IITJEE, Home Tuition available small groups students IB International Baccalaureate Programme IGCSE International General Certificate Secondary Education ISc Indian School Certificate ICSE Indian Certificate of Secondary Education CBSE Central Board of Secondary Education The Schools offering IB International Baccalaureate Programme Bangalore International School Geddalahalli Hennur Bagalur Road Kothanur Post Bengaluru India 560 077 Stonehill International School, 1st Floor, Embassy Point #150, Infantry Road Bengaluru 560 001 Stonehill International School 259/333/334/335, Tarahunise Post Jala Hobli, Bengaluru North 562157 Candor International School Begur – Koppa Road, Hullahalli, Off Bannerghatta Road, Near Electronic City, Bangalore – 560105 Greenwood High International School Bengaluru No.8-14, Chickkawadayarapura, Near Heggondahalli, Gunjur Post, Varthur Sarjapur Road, Bangalore-560087 Sarla Birla Academy Bannerghatta, Bangalore, Canadian International School, Yelahanka, Bangalore Indus International School, Billapura Cross, Sarjapur Bangalore IGCSE International General Certificate of Secondary Education ) Schools of Bangalore Greenwood high international school, No.8-14, Chickkawadayarapura Gunjur Post, Varthur Sarjapur Road, Bangalore Oakridge International School, Oakridge International School, Sarjapur Road, Bangalore Edify School Electronic City 105 34th Main 23rd Cross Sector-A Surya Nagar Phase-2, Anekal-Chandapura Main Road, Electronic City Bangalore Orchids The International School Jalahalli Nagarbavi Mysore Road Sarjapur Road BTM, Bangalore Trio World School, #3/5, Kodigehalli Main Road Sahakar Nagar, Bangalore Ekya School, No.16, 6TH B Main J P Nagar 3RD Phase, Bangalore Vibgyor High school, 58/1, Thubarahallli Whitefield Road, Bangalore Vidyashilp Academy, 42/3, Shivanahalli Yelahanka, Bangalore, PRIMUS Public School, Post Box No. 21, Chikanayakanahalli Village, Off. Sarjapur Road Bangalore Jain International Residential School Jakkasandra Post, Kanakapura Taluk Bangalore Ryan International School, Kundanahalli, M. H. Colony, AECS Layout, Kundalahalli Gate,Bhd Hindustan Lever Ltd, Marathahalli Colony, Bangalore Ebenezer International School, Singena Agrahara Road, Via Hosur Road / A.P.M.C. Yard, Bangalore Mallya Aditi International School, Yelahanka Bangalore India International school 26/1,Chikkabellandur, Carmel Ram Post, Bangalore Ryan International School, Yelahanka, Vederapura Village, Gentiganahalli Road, Training Centre, Yelahanka Bangalore Indus International School, Billapura Cross Sarjapur, Bangalore The International School Bangalore (TISB), NAFL Valley Whitefield – Sarjapur Road, Bangalore Treamis World School, Hulimangala Post Bangalore Ryan International School, Bannerghatta road, Opp. Confident Cascade Bannergatta Main Road Bangalore International School, Geddalahalli Hennur Bagalur Road, Kothanur Post Bangalore Sarla Birla Academy Bannerghatta Jigni Road Bangalore Inventure Academy Whitefield – Sarjapur Road Bangalore Prakriya, # 70, Chikkanayakanahalli Road off Doddakannelli Sarjapur Road, Bangalore Buddhi School, 57, 3rd Main, 4th Cross RMV 2nd Stage, H.I.G Colony, Bangalore B.G.S. International Residential School Nithyananda Nagar, Kumbalagudu, Gollahalli Kengeri, Bangalore Solutions, India, IPhO, APhO, IMO, RMO, INMO, through, lectures, problems numericals Zookeeper, Subhashish, Chattopadhyay, Projectile, Latent, Heat Thermodynamics std 11 12 ISc Calculus BE BTech Differentiation Integration Mechanics Surface Tension Viscosity Accelerating Frame velocity wedge mass pulley Moment Inertia Roorkey Joint Entrance Exam CET AIEEE Irodov HCV Verma South Bangalore Intermediate Algebra Trigonometry Sexy Free Coaching study material preparation Olympiad Friction sin Modelling cos Potential tan cot Gravitation Electrostatics sec Field cosec Ellipse Parabola Hyperbola inverse string Tuition Kinetic Theory Gases Isothermal Adiabatic Isochoric Isobaric Processes Root Mean Square Differential Equation Soomrit Specific Cp Cv PV Diagram Bending Stress Strain Geostationary Satellite Entropy Coefficient Linear Expansion Alpha Beta Gamma Pendulum Conductivity Latent ice water Hydrometer Glass tube series Parallel travelling standing wave Sound Radiation stefan Boltzmann law Newton cooling cylinder Harmonic Overtone Resonance Sonometer Kunds Beat Frequency vibration tuning Fork Swimmer Young Bulk Modulus welded chamber not similar dissimilar MIT Caltech Yale pipe Magnetic Tesla Lenz LvB Vijaya Bank Enclave Apartments Bannerghatta Road Behind IIM Jayanagar J-P-Nagar Buoyant Buoyancy Rho efflux Bernoullis rare Poiseuilles Torricellis critical Terminal Reynolds Poise coalescing Laplace Ventury Hoop orifice Siphon Foucault stretched compression ball scale constant length shear poisson Ratio clock loosing time tvanausdal1 vkiledj Density Partial Pressure Humidity Leak SmartlearnwebTV Space Puncture Photon RC RLC LR Circuit Electrical Capacitor Inductance Linked Flux Wheatstone Bridge Freelanceteach Troutons Rule Van Arkel Method Overview Metallurgy Roasting Calcination Froth Floatation Purification Projected Area PET Kerala MPPET Delta Star conversion Internal Resistance Battery Trick Questions Infinite Ladder Quadratic Cubic Quartic Quintic Orissa NSEP ckt eqn mesh Folding Lenzs J&K Karnataka RMS instantaneous BCECE Maharastra MHCET RPET stepup stepdown transformer Bilekahalli UPSEAT shunt galvanometer susceptibility oscillating magnetometer pole strength Bihar Rajasthan Uttarpradesh Punjab Hariana TN Tamilnadu Andhra WB west Bengal Vacuum Diode Triode Rectifier Truth Table Thermionic emission, Radioactivity Half Life Langmiur, Child Law FCC BCC Cube Optics Lens Mirror Focus Focal Concave Convex Lux Phot Lumen Double slit Complex Integral coordinate Geometry compounds, Biochemistry, Plastic, Organic Chemistry Physical Analytical Inorganic Metallurgy, Biotechnology, Polymer Science, Rubber Technology Geology, Pharma, Veterinary Science,Food Technology, Cryogenics, Ceramics acid species IITJEE SKMClasses.weebly.com proton donor activation energy minimum energy IITJEE SKMClasses.weebly.com reaction breaking bonds addition polymer very long molecular chain formed repeated addition reactions many unsaturated alkene molecules monomers addition polymerisation process unsaturated alkene molecules monomers add growing polymer chain one timeIITJEE SKMClasses.weebly.com long saturated molecular chain addition polymer addition reaction reaction IITJEE SKMClasses.weebly.com reactant added IITJEE SKMClasses.weebly.com unsaturated molecule saturated molecule adsorption process IITJEE SKMClasses.weebly.com occurs gas, liquid solute surface solid rarely liquid alicyclic hydrocarbon hydrocarbon IITJEE SKMClasses.weebly.com carbon atoms joined together ring structure aliphatic hydrocarbon hydrocarbon IITJEE SKMClasses.weebly.com carbon atoms joined together straight branched chains alkali type base IITJEE SKMClasses.weebly.com dissolves water forming hydroxide ions OH (aq) ions alkanes homologous series IITJEE SKMClasses.weebly.com general formula C alkyl group alkane IITJEE SKMClasses.weebly.com hydrogen atom removed CH alkyl groups IITJEE SKMClasses.weebly.com IITJEE skmclasses.weebly.com ‘R’ amount substance quantity whose unit mole Chemists amount substance IITJEE skmclasses.weebly.com IITJEE counting atoms anhydrous substance IITJEE SKMClasses.weebly.com contains water molecules anion negatively charged ion atom economy atomic orbital region within atom hold two electrons IITJEE SKMClasses.weebly.com opposite spins atomic proton number number protons nucleus atom 100 products masses molecular sum product desired mass molecular economy atom Chemistry average bond enthalpy average enthalpy change IITJEE SKMClasses.weebly.com place IITJEE SKMClasses.weebly.com breaking homolytic fission 1 molIITJEE SKMClasses.weebly.com type bond molecules gaseous species Avogadro constant,isotope number atoms mole carbon base species IITJEE SKMClasses.weebly.com proton acceptor biodegradable material substance IITJEE SKMClasses.weebly.com broken IITJEE SKMClasses.weebly.com naturally environment living organisms Boltzmann distribution distribution energies molecules particular temperature IITJEE skmclasses.weebly.com graph bond enthalpy enthalpy change IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com breaking homolytic fission 1 mol bond molecules gaseous species carbanion organic ion IITJEE SKMClasses.weebly.com carbon atom hIITJEE skmclasses.weebly.com negative charge carbocation organic ion IITJEE SKMClasses.weebly.com carbon atom hIITJEE skmclasses.weebly.com positive charge catalyst substance IITJEE SKMClasses.weebly.com increases rate chemical reaction process cation positively charged ion cis trans isomerism special type isomerism IITJEE SKMClasses.weebly.com non hydrogen group skmclasses.weebly.com hydrogen atom C C=C double bond cis isomer ( Z isomer) IITJEE skmclasses.weebly.com H atoms on IITJEE SKMClasses.weebly.com carbon same side trans isomer E isomer H atoms carbon different bond compound substance formed IITJEE SKMClasses.weebly.com two IITJEE SKMClasses.weebly.com chemically bonded elements fixed ratio, usually chemical formula concentration amount solute mol IITJEE SKMClasses.weebly.com 1 dm 3 1000 cm solution coordinate bond shared pair electrons provided one bonding atoms called dative covalent bond covalent bond bond formed shared pair electrons cracking breaking long chained saturated hydrocarbonsIITJEE SKMClasses.weebly.com mixture shorter chained alkanesalkenes curly arrow symbol IITJEE SKMClasses.weebly.com reaction mechanisms IITJEE SKMClasses.weebly.com show movement electron Coaching ICWA Coaching CFA Coaching CFP Coaching CMAT Coaching School Tuitions CBSE School Tuitions Home Tuitions 9th STD Tuitions PUC Coaching 10th Std Tuitions College Tuitions Maths Tuitions Engineering Tuitions Accounts & Finance Tuitions MBA & BBA Coaching Microbiology & Biotech Tuitions Study Abroad GRE & SAT Coaching GMAT Coaching IELTS/TOEFL Coaching PTE Coaching proteins protonation pyridines pyrroles quinones quinolines radical reaction radicals rearrangement receptors reduction regioselectivity retro reaction rhodium ring closure ring contraction ring expansion ring opening ruthenium samarium scandium Schiff bases selenium self-assembly silicon sodium solid-phase synthesis solvent effects spectroscopy sphingolipids spiro compounds stereoselective synthesis stereoselectivity steric hindrance steroids Stille reaction substituent effects sulfates sulfonamides sulfones sulfoxides sulfur supported catalysis supramolecular tandem reaction tautomerism terpenoids thioacetals thiols tin titanium total synthesis transesterification transition metals transition states tungsten Umpolung vinylidene complexes vitamins Wacker reaction Wittig reaction ylides zeolites zinc BRST Quantization Effective field theories Field Theories Higher Dimensions Field Theories Lower Dimensions Large Extra Dimensions Lattice Quantum Field Theory Nonperturbative Effects Renormalization Group Renormalization Regularization skmclasses.weebly.com Renormalons Sigma Models Solitons Monopoles skmclasses.weebly.com Instantons Supersymmetric gauge theory Topological Field Theories 1/N Expansion Anyons Chern-Simons Theories Confinement Duality Gauge Field Theories Lattice Gauge Field Theories Scattering Amplitudes Spontaneous Symmetry Breaking Strong Coupling Expansion Topological States Matter Wilson ‘t Hooft skmclasses.weebly.comPolyakov loops Anomalies Field skmclasses.weebly.comString Theories BRST Symmetry Conformal skmclasses.weebly.com W Symmetry Discrete skmclasses.weebly.comFinite Symmetries Gauge Symmetry Global Symmetries Higher Spin Symmetry Space-Time Symmetries AdS-CFT Correspondence Black Holes String Theory Bosonic Strings Brane Dynamics Gauge Theories Conformal Field Models String Theory D-branes dS vacua string theory F-Theory Flux compactifications Gauge-gravity correspondence Holography skmclasses.weebly.comcondensed matter physics (AdS CMT) Holography skmclasses.weebly.comquark-gluon plasmas Intersecting branes models Long strings M(atrix) Theories M-Theory p-branes Penrose limit skmclasses.weebly.compp-wave background String Duality String Field Theory String theory skmclasses.weebly.comcosmic string Superstring Vacua Superstrings skmclasses.weebly.comHeterotic Strings Tachyon Condensation Topological Strings 2D Gravity Black Holes Classical Theories Gravity Higher Spin Gravity Lattice Models Gravity Models Quantum Gravity Spacetime Singularities Extended Supersymmetry Supergravity Models Superspaces Supersymmetric Effective Theories Supersymmetry skmclasses.weebly.com Duality Supersymmetry Breaking Differential skmclasses.weebly.comAlgebraic Geometry Integrable Hierarchies Non-Commutative Geometry Quantum Groups Statistical Methods Stochastic Processes Cosmology Theories beyond SM Solar skmclasses.weebly.comAtmospheric Neutrinos Thermal Field Theory Be Ansatz Boundary Quantum Field Theory Exact S-Matrix Quantum Dissipative Systems Random Systems B-Physics Beyond Standard Model Compactification skmclasses.weebly.com String Models CP violation Electromagnetic Processes skmclasses.weebly.com Properties GUT Heavy Quark Higgs Kaon LEP HERA skmclasses.weebly.com SLC Neutrino Physics Quark Masses skmclasses.weebly.comSM Parameters Rare Decays Standard Model Supersymmetric Standard Model Technicolor skmclasses.weebly.com Composite Models Chiral Lagrangians Deep Inelastic Scattering Higher Twist Effects Lattice QCD Parton Model Phase Diagram QCD Phenomenological Models QCD Quark-Gluon Plasma Resummation Sum Rules Aim Global Education Koramangala Computer Networking Training Cloud Computing Training JBOSS Training Juniper Certification Training L2 & L3 Protocol Training MCTS Training Engineering design Training CAD & CAM Training MATLAB Training PLC Training SCADA Training VLSI Design Multimedia & Design Training 2D Animation Training 3D Animation Training 4D Animation Training CorelDRAW Training VFX Training Web Technologies Training ASP.Net Training JQuery pair breaking formation covalent bond dative covalent shared pair electrons IITJEE SKMClasses.weebly.com hIITJEE skmclasses.weebly.com been provided one bonding atoms only IITJEE SKMClasses.weebly.com called coordinate bond dehydration elimination reaction IITJEE SKMClasses.weebly.com water removed saturated molecule IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com unsaturated molecule delocalised Electrons IITJEE SKMClasses.weebly.com shared IITJEE SKMClasses.weebly.com two atoms displacement reaction reaction IITJEE SKMClasses.weebly.com reactive element displaces less reactive element IITJEE SKMClasses.weebly.com aqueous solution latter’s ions displayed formula showing relative positioning atoms molecule skmclasses.weebly.com bonds IITJEE SKMClasses.weebly.com disproportionation oxidation skmclasses.weebly.com reduction element redox reaction dynamic equilibrium equilibrium IITJEE SKMClasses.weebly.com exists closed system IITJEE SKMClasses.weebly.com rate forward reaction equal IITJEE SKMClasses.weebly.com rate reverse reaction E/Z isomerism type stereoisomerism IITJEE SKMClasses.weebly.com different groups attached IITJEE SKMClasses.weebly.com carbon C=C double bond arranged differently space restricted rotation C=C bond electron configuration arrangement electrons IITJEE SKMClasses.weebly.com atom electronegativity measure attraction bonded atom skmclasses.weebly.com pair electrons covalent bond electron shielding repulsion IITJEE SKMClasses.weebly.com electrons different inner shells Shielding reduces net attractive force IITJEE SKMClasses.weebly.com positive nucleus outer shell electrons electrophile atom group atoms IITJEE SKMClasses.weebly.com attracted IITJEE SKMClasses.weebly.com electron rich centre atom IITJEE SKMClasses.weebly.com accepts pair electrons covalent bond electrophilic addition type addition reaction IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com electrophile attracted electron rich centre atom accepts pair electrons IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com new covalent bond elimination reaction removal molecule IITJEE SKMClasses.weebly.com saturated molecule IITJEE SKMClasses.weebly.com unsaturated molecule empirical formula simplest whole number ratio atoms IITJEE SKMClasses.weebly.com element present compound endothermic reaction reaction IITJEE SKMClasses.weebly.com enthalpy products greater enthalpy reactants resulting heat being taken surroundings enthalpy heat content IITJEE SKMClasses.weebly.com stored chemical system standard enthalpy change combustion enthalpy change IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com one mole substance reacts completely IITJEE SKMClasses.weebly.com oxygen under standard conditions reactants skmclasses.weebly.com products being IITJEE SKMClasses.weebly.com standard states (standard) enthalpy change formation enthalpy change IITJEE SKMClasses.weebly.com one mole compound formed IITJEE SKMClasses.weebly.com constituent elements IITJEE SKMClasses.weebly.com standard states under standard conditions (standard) enthalpy change reaction enthalpy change IITJEE SKMClasses.weebly.com accompanies reaction molar quantities expressed chemical equation under standard conditions reactants skmclasses.weebly.com products being IITJEE SKMClasses.weebly.com standard states enthalpy cycle diagram showing alternative routes IITJEE SKMClasses.weebly.com reactants products IITJEE SKMClasses.weebly.com allows indirect determination IITJEE SKMClasses.weebly.com enthalpy change IITJEE SKMClasses.weebly.com other known enthalpy changes using Hess’ law enthalpy profile diagram skmclasses.weebly.com reaction IITJEE SKMClasses.weebly.com compare enthalpy reactants IITJEE SKMClasses.weebly.com enthalpy products esterification reaction IITJEE SKMClasses.weebly.com alcohol IITJEE SKMClasses.weebly.com carboxylic acid IITJEE SKMClasses.weebly.com produce ester skmclasses.weebly.com water exothermic reaction IITJEE SKMClasses.weebly.com enthalpy products smaller enthalpy reactants, resulting heat loss IITJEE SKMClasses.weebly.com surroundings fractional distillation separation components liquid mixture skmclassesfractions IITJEE SKMClasses.weebly.com differ boiling point skmclasses.weebly.com hence chemical composition IITJEE SKMClasses.weebly.com distillation typically using fractionating column fragmentation process mass spectrometry IITJEE SKMClasses.weebly.com causes positive ion split skmclasses pieces one positive fragment ion functional group part organic molecule responsible skmclasses.weebly.com chemical reactions general formula simplest algebraic formula member homologous series. skmclasses.weebly.com example general formula alkanes giant covalent lattice dimensional structure atoms, bonded together strong covalent bonds giant ionic lattice three dimensional structure oppositely charged ions, bonded together strong ionic bonds giant metallic lattice three dimensional structure positive ions skmclasses.weebly.com delocalised electrons, bonded together strong metallic bonds greenhouse effect process IITJEE SKMClasses.weebly.com absorption subsequent emission infrared radiation atmospheric gases warms lower atmosphere planet’s surface group vertical column Periodic Table Elements group IITJEE SKMClasses.weebly.com similar chemical properties skmclasses.weebly.com atoms skmclasses.weebly.comnumber outer shell electrons Hess law reaction IITJEE SKMClasses.weebly.com one route skmclasses.weebly.com initial final conditions IITJEE SKMClasses.weebly.com skmclasses.weebly.com total enthalpy change skmclasses.weebly.com skmclasses.weebly.com route heterogeneous catalysis reaction IITJEE SKMClasses.weebly.com catalyst IITJEE skmclasses.weebly.com different physical state reactants; frequently, reactants IITJEE SKMClasses.weebly.com gases whilst catalyst solid heterolytic fission breaking covalent bond IITJEE SKMClasses.weebly.com both bonded electrons going IITJEE SKMClasses.weebly.com one atoms, forming cation (+ ion) skmclasses.weebly.com IITJEE SKMClasses.weebly.com anion ion homogeneous catalysis reaction catalyst skmclasses.weebly.com reactants physical state, IITJEE SKMClasses.weebly.com frequently aqueous gaseous state homologous series series organic compounds IITJEE SKMClasses.weebly.com skmclasses.weebly.com functional group, IITJEE SKMClasses.weebly.com successive member differing homolytic fission breaking covalent bond IITJEE SKMClasses.weebly.com one bonded electrons going IITJEE SKMClasses.weebly.com atom, forming two radicals hydrated Crystalline skmclasses.weebly.com containing water molecules hydrocarbon compound hydrogen skmclasses.weebly.com carbon hydrogen bond strong dipole attraction IITJEE SKMClasses.weebly.com electron deficient hydrogen atom (O H on different molecule hydrolysis reaction IITJEE SKMClasses.weebly.com water aqueous hydroxide ions IITJEE SKMClasses.weebly.com breaks chemical compound skmclasses two compounds initiation first step radical substitution IITJEE SKMClasses.weebly.com free radicals generated ultraviolet radiation intermolecular force attractive force IITJEE SKMClasses.weebly.com neighbouring molecules Intermolecular forces van der Waals’ forces induced dipole ces permanent dipole forces hydrogen bonds ion positively negatively charge atom covalently bonded group atoms molecular ion ionic bonding electrostatic attraction IITJEE SKMClasses.weebly.com oppositely charged ions first) ionisation energy IITJEE SKMClasses.weebly.com remove one electron IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com ion one mole gaseous 1+ ions IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com one mole gaseous 2+ ions second) ionisation energy IITJEE SKMClasses.weebly.com remove one electron IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com ion one mole gaseous 1+ ions IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com one mole gaseous 2+ ions successive ionisation measure energy IITJEE SKMClasses.weebly.com remove IITJEE SKMClasses.weebly.com electron Chemistry energy second ionisation energy energy IITJEE SKMClasses.weebly.com one electron IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com ion one mole gaseous 1+ ions IITJEE SKMClasses.weebly.com one mole gaseous 2+ ions isotopes Atoms skmclasses.weebly.com element IITJEE SKMClasses.weebly.com different numbers neutrons different masses le Chatelier’s principle system dynamic equilibrium subjected change position equilibrium will shift minimise change limiting reagent substance chemical reaction IITJEE SKMClasses.weebly.com runs out first lone pair outer shell pair electrons IITJEE SKMClasses.weebly.com involved chemical bonding mass nucleon number particles protons aneutrons) nucleus mechanism sequence steps showing path taken electrons reaction metallic bond electrostatic attraction IITJEE SKMClasses.weebly.com positive metal ions adelocalised electrons molar mass substance units molar mass IITJEE SKMClasses.weebly.com molar volume IITJEE SKMClasses.weebly.com mole gas. units molar volume IITJEE SKMClasses.weebly.com dm room temperature skmclasses.weebly.com pressure molar volume approximately 24.0 substance containing IITJEE skmclasses.weebly.com many particles thereIITJEE SKMClasses.weebly.com carbon atoms exactly 12 g carbon isotope molecular formula number atoms IITJEE SKMClasses.weebly.com element molecule molecular ion M positive ion formed mass spectrometry IITJEE SKMClasses.weebly.com molecule loses electron molecule small group atoms held together covalent bonds monomer small molecule IITJEE SKMClasses.weebly.com combines IITJEE SKMClasses.weebly.com monomers polymer nomenclature system naming compounds nucleophile atom group atoms attracted electron deficient centre atom donates pair electrons covalent bond nucleophilic substitution type substitution reaction IITJEE SKMClasses.weebly.com nucleophile attracted electron deficient centre atom, IITJEE SKMClasses.weebly.com donates pair electrons IITJEE SKMClasses.weebly.com new covalent bond oxidation Loss electrons IITJEE SKMClasses.weebly.com increase oxidation number oxidation number measure number electrons IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com atom uses bond IITJEE SKMClasses.weebly.com atoms another element. Oxidation numbers IITJEE SKMClasses.weebly.com derive d rules oxidising agent reagent IITJEE SKMClasses.weebly.com oxidises (takes electrons from) another species percentage yield period horizontal row elements Periodic Table Elements show trends properties across period periodicity regular periodic variation properties elements IITJEE SKMClasses.weebly.com atomic number position Periodic Table permanent dipole small charge difference across bond resulting IITJEE SKMClasses.weebly.com difference electronegativities bonded atoms permanent dipole dipole force attractive force IITJEE SKMClasses.weebly.com permanent dipoles neighbouring polar molecules pi bond (p bond reactive part double bond formed above skmclasses.weebly.com below plane bonded atoms sideways overlap p orbitalspolar covalent bond bond IITJEE SKMClasses.weebly.com permanent dipole polar molecule molecule IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com overall dipole skmclasses account dipoles across bonds polymer long molecular chain built monomer units precipitation reaction formation solid solution during chemical reaction Precipitates IITJEE SKMClasses.weebly.com formed IITJEE SKMClasses.weebly.com two aqueous solutions IITJEE SKMClasses.weebly.com mixed together principal quantum number n number representing relative overall energy orbital IITJEE SKMClasses.weebly.com increases distance nucleus sets orbitals IITJEE SKMClasses.weebly.com value IITJEE skmclasses.weebly.com electron shells energy levels propagation two repeated radical substitution IITJEE SKMClasses.weebly.com build up products chain reaction radical species unpaired electron rate reaction change concentration reactant product redox reaction reaction IITJEE SKMClasses.weebly.com reduction skmclasses.weebly.com oxidation take IITJEE SKMClasses.weebly.com reducing agent reagent IITJEE SKMClasses.weebly.com reduces (adds electron to) species reduction Gain electrons decrease oxidation number yield actual amount mol product theoretical amount mol product Chemistry reflux continual boiling skmclasses.weebly.com condensing reaction mixture ensure IITJEE SKMClasses.weebly.com reaction IITJEE SKMClasses.weebly.com without contents flask boiling dry relative atomic mass weighted mean mass atom element compared one twelfth mass IITJEE SKMClasses.weebly.com atom carbon relative formula mass weighted mean mass formula unit compared IITJEE SKMClasses.weebly.com one twelfth mass atom carbon relative isotopic mass mass atom isotope compared IITJEE SKMClasses.weebly.com one twelfth mass atom carbon relative molecular mass weighted mean mass molecule compared twelfth mass atom carbon 12 repeat unit specific arrangement atom s IITJEE SKMClasses.weebly.com occurs structure over over again. Repeat units IITJEE SKMClasses.weebly.com included brackets outside IITJEE SKMClasses.weebly.com symbol n Salt chemical compound formed IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com acid IITJEE SKMClasses.weebly.com H+ ion acid IITJEE skmclasses.weebly.com been replaced metal ion another positive ion such IITJEE skmclasses.weebly.com ammonium ion, NH saturated hydrocarbon IITJEE SKMClasses.weebly.com single bonds only shell group atomic orbitals IITJEE SKMClasses.weebly.com skmclasses.weebly.com principal quantum number known main energy level simple molecular lattice three dimensional structure molecules, bonded together weak intermolecular forces skeletal formula simplified organic formula, IITJEE SKMClasses.weebly.com hydrogen atoms removed alkyl chains, leaving carbon skeleton skmclasses.weebly.com associated functional groups species particle IITJEE SKMClasses.weebly.com part chemical reaction specific heat capacity, c energy IITJEE SKMClasses.weebly.com raise temperature 1 g substance 1 C spectator ions Ions present part chemical reaction standard conditions pressure 100 kPa 1 atmosphere stated temperature usually 298 K (25 °C), skmclasses.weebly.com concentration 1 mol dm reactions aqueous solutions standard enthalpies enthalpystandard solution solution known concentration Standard solutions normally IITJEE SKMClasses.weebly.com titrations IITJEE SKMClasses.weebly.com determine unknown information another substance Chemistry standard state physical state substance under standard conditions 100 kPa 1 atmosphere) skmclasses.weebly.com 298 K 25 C stereoisomers Compounds skmclasses.weebly.com structural formula IITJEE SKMClasses.weebly.com different arrangement atoms space stoichiometry molar relationship IITJEE SKMClasses.weebly.com relative quantities substances part reaction stratosphere second layer Earth’s atmosphere, containing ‘ozone layer’, about 10 km IITJEE SKMClasses.weebly.com 50 km above Earth’s surface structural formula formula showing minimal detail skmclasses.weebly.com arrangement atoms molecule structural isomers Molecules IITJEE SKMClasses.weebly.com skmclasses.weebly.com molecular formula different structural arrangements atoms subshell group skmclasses.weebly.com type atomic orbitals s, p, d f within shell substitution reaction reaction IITJEE SKMClasses.weebly.com atom group atoms replaced different atom group atoms termination step end radical substitution IITJEE SKMClasses.weebly.com two radicals combine IITJEE SKMClasses.weebly.com molecule thermal decomposition breaking chemical substance IITJEE SKMClasses.weebly.com heat skmclasses least two chemical substances troposphere lowest layer Earth’s atmosphere extending Earth’s surface about 7 km (above poles) about 20 km above tropics unsaturated hydrocarbon hydrocarbon containing carbon carbon multiple bonds van der Waals’ forces Very weak attractive forces IITJEE SKMClasses.weebly.com induced dipoles neighbouring molecules volatility ease IITJEE SKMClasses.weebly.com liquid turns skmclasses gas Volatility increases boiling point decreases water crystallisation Water molecules IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com essential part crystalline structure absolute zero – theoretical condition concerning system at zero Kelvin IITJEE SKMClasses.weebly.com system does IITJEE SKMClasses.weebly.com emit absorb energy (all atoms rest accuracy – how close value IITJEE SKMClasses.weebly.com actual true value IITJEE SKMClasses.weebly.com see precision acid compound that, IITJEE SKMClasses.weebly.com dissolved water pH less 7.0 compound IITJEE SKMClasses.weebly.com donates hydrogen ion acid anhydride compound IITJEE SKMClasses.weebly.com two acyl groups boundIITJEE SKMClasses.weebly.com single oxygen atom acid dissociation constant – IITJEE SKMClasses.weebly.com equilibrium constant skmclasses.weebly.com dissociation weak acid actinides – fifteen chemical elements IITJEE SKMClasses.weebly.com actinium (89) skmclasses.weebly.com lawrencium (103 activated complex – structure IITJEE SKMClasses.weebly.com forms because collisionIITJEE SKMClasses.weebly.com molecules new bondsvIITJEE SKMClasses.weebly.com formed activation energy – minimum energy IITJEE SKMClasses.weebly.com must be inputIITJEE SKMClasses.weebly.com chemical system activity series actual yield addition reaction – within organic chemistry, IITJEE SKMClasses.weebly.com two IITJEE SKMClasses.weebly.com molecules combineIITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com larger aeration mixing air skmclasses liquid solid alkali metals metals Group 1 on periodic table alkaline earth metals – metals Group 2 on periodic table allomer substance IITJEE SKMClasses.weebly.com hIITJEE skmclasses.weebly.comdifferent composition another skmclasses.weebly.comcrystalline structure allotropy elements IITJEE SKMClasses.weebly.com different structures skmclasses.weebly.com therefore different forms IITJEE skmclasses.weebly.com Carbon diamonds, graphite, skmclasses.weebly.com fullerene anion negatively charge ions anode – positive side dry cell battery cell aromaticity – chemical property conjugated rings IITJEE SKMClasses.weebly.com results unusual stability. See IITJEE SKMClasses.weebly.com benzene atom – chemical element IITJEE SKMClasses.weebly.com smallest form, skmclasses.weebly.com made up neutrons skmclasses.weebly.comprotons within nucleus skmclasses.weebly.comelectrons circling nucleus atomic mass unit atomic number number representing IITJEE SKMClasses.weebly.com element IITJEE SKMClasses.weebly.com corresponds IITJEE SKMClasses.weebly.com number protons within nucleus atomic orbital region IITJEE SKMClasses.weebly.com electron atom may be found atomic radius average atomic mass Avogadro’s law Avogadro’s number number particles mole substance ( 6.02×10^23 ) barometer deviceIITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com measure pressure atmosphere base substance IITJEE SKMClasses.weebly.com accepts proton skmclasses.weebly.com high pH; common example sodium hydroxide (NaOH biochemistry chemistry organisms boiling phase transition liquid vaporizing boiling point temperature IITJEE SKMClasses.weebly.com substance startsIITJEE SKMClasses.weebly.com boil boiling-point elevation process IITJEE SKMClasses.weebly.com boiling point elevated adding substance bond – attraction skmclasses.weebly.com repulsion IITJEE SKMClasses.weebly.com atoms skmclasses.weebly.com molecules IITJEE SKMClasses.weebly.com cornerstone Boyle’s law Brønsted-Lowrey acid chemical species IITJEE SKMClasses.weebly.com donates proton Brønsted–Lowry acid–base reaction Brønsted-Lowrey base – chemical species IITJEE SKMClasses.weebly.com accepts proton buffered solution – IITJEE SKMClasses.weebly.com aqueous solution consisting weak acid skmclasses.weebly.comits conjugate base weak base skmclasses.weebly.comits conjugate acid IITJEE SKMClasses.weebly.com resists changes pH IITJEE SKMClasses.weebly.com strong acids basesIITJEE SKMClasses.weebly.com added burette (IITJEE SKMClasses.weebly.com buret glasswareIITJEE SKMClasses.weebly.com dispense specific amounts liquid IITJEE SKMClasses.weebly.com precision necessary titration skmclasses.weebly.com resource dependent reactions example combustion catalyst chemical compoundIITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com change rate IITJEE SKMClasses.weebly.com speed up slow down reaction,IITJEE SKMClasses.weebly.com regenerated at end reaction cation – positively charged ion centrifuge equipmentIITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com separate substances based on density rotating tubes around centred axis cell potential force galvanic cell IITJEE SKMClasses.weebly.com pulls electron through reducing agentIITJEE SKMClasses.weebly.com oxidizing agent chemical Law certain rules IITJEE SKMClasses.weebly.com pertain IITJEE SKMClasses.weebly.com laws nature skmclasses.weebly.comchemistry – examples chemical reaction – change one IITJEE SKMClasses.weebly.com substances skmclassesanother multiple substances colloid mixture evenly dispersed substances such IITJEE skmclasses.weebly.comm milks combustion IITJEE SKMClasses.weebly.com exothermic reaction IITJEE SKMClasses.weebly.com oxidant skmclasses.weebly.comfuel IITJEE SKMClasses.weebly.com heat skmclasses.weebly.comoften light compound – substance IITJEE SKMClasses.weebly.com made up two IITJEE SKMClasses.weebly.com chemically bonded elements condensation phase changeIITJEE SKMClasses.weebly.com gasIITJEE SKMClasses.weebly.com liquid conductor material IITJEE SKMClasses.weebly.com allows electric flow IITJEE SKMClasses.weebly.com freely covalent bond – chemical bond IITJEE SKMClasses.weebly.com involves sharing electrons crystal solid IITJEE SKMClasses.weebly.com packed IITJEE SKMClasses.weebly.com ions, molecules atoms IITJEE SKMClasses.weebly.com orderly fashion cuvette glasswareIITJEE SKMClasses.weebly.com spectroscopic experiments. usually made plastic glass quartz skmclasses.weebly.comshould be IITJEE possible deionization removal ions, skmclasses.weebly.com water’s case mineral ions such IITJEE skmclasses.weebly.comsodium, iron skmclasses.weebly.comcalcium deliquescence substances IITJEE SKMClasses.weebly.com absorb water IITJEE SKMClasses.weebly.com atmosphereIITJEE SKMClasses.weebly.com liquid solutions deposition – settling particles within solution mixture dipole electric magnetic separation charge dipole moment – polarity polar covalent bond dissolution solvation – spread ions monosacharide double bond sharing two pairs electradodes Microcentrifuge Eppendorf tube IITJEE SKMClasses.weebly.com Coomassie Blue solution earth metal – see alkaline earth metal electrolyte solution IITJEE SKMClasses.weebly.com conducts certain amount current skmclasses.weebly.com split categorically IITJEE skmclasses.weebly.com weak skmclasses.weebly.comstrong electrolytes electrochemical cell using chemical reaction’s current electromotive force made electromagnetic radiation type wave IITJEE SKMClasses.weebly.com through vacuums IITJEE skmclasses.weebly.comwell IITJEE skmclasses.weebly.commaterial skmclasses.weebly.comclassified IITJEE skmclasses.weebly.com self-propagating wave electromagnetism fields IITJEE SKMClasses.weebly.com electric charge skmclasses.weebly.comelectric properties IITJEE SKMClasses.weebly.com change way IITJEE SKMClasses.weebly.com particles move skmclasses.weebly.com interact electromotive force device IITJEE SKMClasses.weebly.com gains energy IITJEE skmclasses.weebly.comelectric charges pass through electron – subatomic particle IITJEE SKMClasses.weebly.com net charge IITJEE SKMClasses.weebly.com negative electron shells – IITJEE SKMClasses.weebly.com orbital around atom’s nucleus fixed number electrons usually two eight electric charge measured property (coulombs) IITJEE SKMClasses.weebly.com determine electromagnetic interaction element IITJEE SKMClasses.weebly.com atom IITJEE SKMClasses.weebly.com defined IITJEE SKMClasses.weebly.com atomic number energy – system’s abilityIITJEE SKMClasses.weebly.com do work enthalpy – measure total energy thermodynamic system (usually symbolized IITJEE skmclasses.weebly.comH entropy – amount energy IITJEE SKMClasses.weebly.com available skmclasses.weebly.com work closed thermodynamic system usually symbolized IITJEE skmclasses.weebly.com S enzyme – protein IITJEE SKMClasses.weebly.com speeds up catalyses reaction Empirical Formula – IITJEE SKMClasses.weebly.com called simplest formula gives simplest whole -number ratio atoms IITJEE SKMClasses.weebly.com element present compound eppendorf tube – generalized skmclasses.weebly.comtrademarked term skmclasses.weebly.com type tube; see microcentrifuge freezing – phase transitionIITJEE SKMClasses.weebly.com liquidIITJEE SKMClasses.weebly.com solid Faraday constant unit electrical charge widelyIITJEE SKMClasses.weebly.com electrochemistry skmclasses.weebly.comequalIITJEE SKMClasses.weebly.com ~ 96,500 coulombs represents 1 mol electrons, Avogadro number electrons: 6.022 × 1023 electrons. F = 96 485.339 9(24) C/mol Faraday’s law electrolysis two part law IITJEE SKMClasses.weebly.com Michael Faraday published about electrolysis mass substance altered at IITJEE SKMClasses.weebly.com electrode during electrolysis directly proportionalIITJEE SKMClasses.weebly.com quantity electricity transferred at IITJEE SKMClasses.weebly.com electrode mass IITJEE SKMClasses.weebly.com elemental material altered at IITJEE SKMClasses.weebly.com electrode directly proportionalIITJEE SKMClasses.weebly.com element’s equivalent weight frequency number cyclesIITJEE SKMClasses.weebly.com unit time. Unit: 1 hertz = 1 cycleIITJEE SKMClasses.weebly.com 1 second galvanic cell battery made up electrochemical IITJEE SKMClasses.weebly.com two different metals connected salt bridge gas particles container IITJEE SKMClasses.weebly.com no definite shape volume geochemistry – chemistry skmclasses.weebly.comchemical composition Earth Gibbs energy – value IITJEE SKMClasses.weebly.com indicates spontaneity reaction usually symbolized G Cavalier India, Kalyan Nagar halogens Group 7 Periodic Table skmclasses.weebly.comare non-metals heat energy transferredIITJEE SKMClasses.weebly.com one systemIITJEE SKMClasses.weebly.com another thermal interaction jodium – Latin name halogen element iodine Joule SI I.M.S. Learning Resources Pvt. Ltd., Jaya Nagar 4th Block unit energy, defined IITJEE skmclasses.weebly.com newton-meter indicator special compound addedIITJEE SKMClasses.weebly.com solution IITJEE SKMClasses.weebly.com changes color depending on acidity solution; different indicators Giraffe Coaching, Cunningham Road different colors effective pH ranges inorganic compound – compounds IITJEE SKMClasses.weebly.com contain carbon IITJEE SKMClasses.weebly.com exceptions main article inorganic chemistry part chemistry concerned IITJEE SKMClasses.weebly.com inorganic compounds International Union Pure skmclasses.weebly.comApplied Chemistry IUPAC insulator material IITJEE SKMClasses.weebly.com resists flow electric current ion molecule gained lost one IITJEE SKMClasses.weebly.com electron ionic bond electrostatic attractionIITJEE SKMClasses.weebly.com oppositely charged ions ionization breaking up compound skmclassesseparate ions Kinetics sub-field chemistry specializing reaction rates Kinetic energy energy IITJEE SKMClasses.weebly.com object IITJEE SKMClasses.weebly.com motion lanthanides Elements 57 through 71 lattice Unique arrangement atoms molecules crystalline liquid solid Laws thermodynamics liquid state matter IITJEE SKMClasses.weebly.com shape container light Portion electromagnetic spectrum IITJEE SKMClasses.weebly.com visibleIITJEE SKMClasses.weebly.com naked eye. IITJEE SKMClasses.weebly.com called “visible light London dispersion forces weak intermolecular force Law Motion object motion stay motion IITJEE SKMClasses.weebly.com object rest stays rest unless IITJEE SKMClasses.weebly.com unbalanced force acts molecule IITJEE SKMClasses.weebly.com one key components within chemistry Metal Chemical element IITJEE SKMClasses.weebly.com good conductor both electricity skmclasses.weebly.comheat skmclasses.weebly.comforms cations skmclasses.weebly.comionic bonds IITJEE SKMClasses.weebly.com non-metals melting phase changeIITJEE SKMClasses.weebly.com solidIITJEE SKMClasses.weebly.com liquid metalloid substance possessing both properties metals skmclasses.weebly.comnon-metals methylene blue heterocyclic aromatic chemical compound IITJEE SKMClasses.weebly.com molecular formula C16H18N3SCl microcentrifuge plastic container IITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com store small amounts liquid mole – abbreviated mol measurement IITJEE SKMClasses.weebly.com amount substance single mole contains approximately 6.022×1023 units entities mole water contains 6.022×1023 H2O molecules molecule chemically I Beacons Academy, Jaya Nagar 4th Block bonded number atoms IITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com electrically neutral molecular orbital region mIITJEE SKMClasses.weebly.com electron found molecule opposed atom neat Alchemy India Services Pvt. Ltd. Residency Road conditions IITJEE SKMClasses.weebly.com liquid reagent gas performed IITJEE SKMClasses.weebly.com no added solvent cosolvent neutron neutral unit subatomic particle Institute Engineering Studies, Malleswaram net charge neutrino particle IITJEE SKMClasses.weebly.com travel speeds close speed light skmclasses.weebly.comare created IITJEE skmclasses.weebly.com result radioactive decay Brainstorm Consulting Pvt. Ltd., Jaya Nagar 4th Block nucleus centre Ace Creative Learning, Basavanagudi Anegundi Coaching Academy, Malleswaram atom made neutrons skmclasses.weebly.comprotons, IITJEE SKMClasses.weebly.com net positive charge noble gases group 18 elements, those whose outer electron shell filled non-metal Career Launcher, Jaya Nagar 3rd Block element IITJEE SKMClasses.weebly.com metallic nuclear pertainingIITJEE SKMClasses.weebly.com atomic Gate Indian Institute Tutorials J.P. Nagar 2nd Phase nucleus nuclear magnetic resonance spectroscopy technique IITJEE SKMClasses.weebly.com exploits magnetic properties certain nuclei, useful skmclasses.weebly.comidentifying unknown compounds number density measure concentration countable objects atoms molecules space; number volume orbital may referIITJEE SKMClasses.weebly.com either IITJEE SKMClasses.weebly.com atomic orbital molecular orbital organic compound compounds IITJEE SKMClasses.weebly.com contain carbon organic chemistry part chemistry concerned IITJEE SKMClasses.weebly.com organic compounds pH measure acidity basicity solution plasma state matter similar gas certain portion particlesIITJEE SKMClasses.weebly.com ionized other metal metallic elements p-block characterized having combination relatively low melting points less 950 K) skmclasses.weebly.comrelatively high electronegativity values IITJEE SKMClasses.weebly.com 1.6 revised Pauling potential energy stored body system due position force field due toIITJEE SKMClasses.weebly.com configuration precipitate formation solid solution inside another solid during chemical reaction diffusion solid precision close results multiple experimental trials IITJEE SKMClasses.weebly.com accuracy photon carrier electromagnetic radiation wavelength IITJEE skmclasses.weebly.comgamma rays skmclasses.weebly.comradio waves proton positive unit subatomic particle IITJEE SKMClasses.weebly.com positive charge protonation addition proton (H+) atom, molecule ion Quantum mechanics study how atoms, molecules, subatomic particles behave Career Edge India, Hosur Road structured quarks – elementary Eduplot Learning Solutions in Malleswaram particle skmclasses.weebly.com fundamental constituent matter quanta minimum amount bundle energy radiation energy IITJEE SKMClasses.weebly.com waves subatomic particles IITJEE SKMClasses.weebly.com change IITJEE SKMClasses.weebly.com high energyIITJEE SKMClasses.weebly.com low energy states radioactive decay – process unstable atomic nucleus losing energy emitting radiation Raoult’s law reactivity series reagent s-block elements – Group 1 skmclasses.weebly.com2 elements (alkali skmclasses.weebly.comalkaline metals), IITJEE SKMClasses.weebly.com includes Hydrogen skmclasses.weebly.comHelium salts – ionic compounds composed anions skmclasses.weebly.comcations salt bridge – devicesIITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com connection reduction IITJEE SKMClasses.weebly.com oxidation half-cells IITJEE SKMClasses.weebly.com electrochemical cell saline solution – general term skmclasses.weebly.comNaCl water Schrödinger equation – quantum state equation IITJEE SKMClasses.weebly.com represents behaviour GoodIITJEE SKMClasses.weebly.com Excellence, BTM 1st Stage election around IITJEE SKMClasses.weebly.com atom semiconductor IITJEE SKMClasses.weebly.com electrically conductive solid IITJEE SKMClasses.weebly.com conductor insulator single bond – sharing one pair electrons sol suspension solid particles liquid Artificial examples include sol-gels solid – one states matter, IITJEE SKMClasses.weebly.com moleculesIITJEE SKMClasses.weebly.com packed close together,IITJEE SKMClasses.weebly.com resistance movement/deformation skmclasses.weebly.comvolume change Young’s solute part solution IITJEE SKMClasses.weebly.com mixed skmclassessolvent Gate Indian Institute Tutorials in J.P. Nagar 2nd Phase NaCl saline water solution homogeneous mixture made up multiple substances. solutes skmclasses.weebly.comsolvents solvent part solution dissolves solute H2O saline water spectroscopy study radiation skmclasses.weebly.commatter, such IITJEE skmclasses.weebly.com X-ray absorption skmclasses.weebly.comemission spectroscopy speed light speed anything IITJEE SKMClasses.weebly.com zero rest mass (Energyrest = mc² IITJEE SKMClasses.weebly.com m mass skmclasses.weebly.comc speed G.C. Rao Academy in Bull Temple Road light Standard conditions skmclasses.weebly.com temperature skmclasses.weebly.compressure SATP standardisationIITJEE SKMClasses.weebly.com order compare experimental results (25 °C skmclasses.weebly.com 100.000 kPa state matter matter having homogeneous, macroscopic phase; gas, plasma Ria Institute Technology in Marathahalli liquid solidIITJEE SKM Classes.weebly.com well known increasing concentration sublimation – phase transitionIITJEE SKMClasses.weebly.com solidIITJEE SKMClasses.weebly.com limewater fuel gas subatomic particles – particles IITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com smaller atom; examplesIITJEE SKMClasses.weebly.com protons neutrons skmclasses.weebly.comelectrons substance – material IITJEE SKMClasses.weebly.com definite chemical composition Phase diagram showing triple skmclasses.weebly.comcritical points substance talc mineral representing one on Mohs Scale skmclasses.weebly.comcomposed hydrated magnesium silicate IITJEE SKMClasses.weebly.com chemical formula H2Mg3(SiO3)4 Mg3Si4O10(OH)2 temperature – average energy microscopic motions particles theoretical yield yield theory model describing nature phenomenon thermal conductivity property material Communication skmclasses.weebly.com Careers R.M.V. Extn. 2nd Stage conduct heat (often noted IITJEE skmclasses.weebly.com k thermochemistry study absorption release heat within chemical reaction thermodynamics study effects changing temperature, volume pressure work, heat, skmclasses.weebly.com energy on macroscopic scale I-Bas Consulting Pvt. Ltd., Ulsoor thermodynamic stability IITJEE SKMClasses.weebly.com system IITJEE SKMClasses.weebly.com lowest energy state IITJEE SKMClasses.weebly.com environment equilibrium thermometer device measures average energy system titration – process titrating one solution IITJEE SKMClasses.weebly.com another Cavalier India, Kalyan Nagar called volumetric analysis torr unit measure pressure (1 Torr equivalentIITJEE SKMClasses.weebly.com 133.322 Pa 1.3158×10-3 atm transition metal elements IITJEE SKMClasses.weebly.com incomplete d sub-shells IITJEE SKMClasses.weebly.com may referredIITJEE SKMClasses.weebly.com IITJEE skmclasses.weebly.com d-block elements transuranic element – element IITJEE SKMClasses.weebly.com atomic number greater 92; none transuranic elementsIITJEE SKMClasses.weebly.com stable triple bond – sharing three pairs electrons within covalent bond example N2 triple point temperature skmclasses.weebly.compressure three phasesIITJEE SKMClasses.weebly.com skmclasses.weebly.com Water special National IAS Academy, Raja Rajeshwari Nagar phase diagram Tyndall effect effect light scattering colloidal mixture IITJEE SKMClasses.weebly.com one substance dispersed evenly through another suspended particles UN number four digit codeIITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com note hazardous skmclasses.weebly.com flammable substances uncertainty characteristic IITJEE SKMClasses.weebly.com measurement IITJEE SKMClasses.weebly.com involves estimation any amount cannot be exactly reproducible Uncertainty principle knowing Shaping Lives Education Pvt. Ltd., Rajaji Nagar location particle makes momentum uncertain knowing momentum particle makes location uncertain unit cell smallest repeating unit lattice unit factor statements Manhattan Review, Jaya Nagar convertingIITJEE SKMClasses.weebly.com units universal ideal gas constant proportionality constant ideal gas law (0.08206 L·atm/(K·mol)) valence electron outermost electrons IITJEE SKMClasses.weebly.com atom IITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com located electron shells Valence bond theory theory explaining chemical bonding within molecules discussing valencies number chemical bonds formed IITJEE SKMClasses.weebly.com atom van der Waals force – one forces (attraction/repulsion)IITJEE SKMClasses.weebly.com molecules van ‘t Hoff factor – ratio moles particles solutionIITJEE SKMClasses.weebly.com moles solute dissolved vapor IITJEE SKMClasses.weebly.com substance below critical temperature gas phase vapour pressure – pressure vapour over liquid at equilibrium vaporization phase changeIITJEE SKMClasses.weebly.com liquidIITJEE SKMClasses.weebly.com gas viscosity – resistance liquidIITJEE SKMClasses.weebly.com flow (oil) volt one joule workIITJEE SKMClasses.weebly.com coulomb unit electrical potential transferred voltmeter – instrument IITJEE SKMClasses.weebly.com measures cell potential volumetric analysis Endeavor, Jaya Nagar 5th Block titration water – H2O – chemical substance, major part cells skmclasses.weebly.com Earth, skmclasses.weebly.com covalently bonded wave function function describing electron’s position three-dimensional space worknamount force over distance skmclasses.weebly.com terms joules energy X-ray ionizing, electromagnetic radiation gamma skmclasses.weebly.comUV rays X-ray diffraction – method skmclasses.weebly.com establishing structures crystalline solids using singe wavelength X-rays skmclasses.weebly.com looking diffraction pattern X-ray photoelectron spectroscopy spectroscopic technique IITJEE SKMClasses.weebly.com measure composition material yield amount product produced during chemical reaction zone melting way remove impuritiesIITJEE SKMClasses.weebly.com IITJEE SKMClasses.weebly.com element melting skmclasses.weebly.com slowly travel IITJEE SKMClasses.weebly.com ingot (cast) Zwitterion chemical compound whose net charge zero skmclasses.weebly.comhence electrically neutral IITJEE SKMClasses.weebly.com positive skmclasses.weebly.com negative charges due formal charge, owing partial charges IITJEE SKMClasses.weebly.com constituent atoms acetals acylation addition aggregation alcohols aldehydes aldol reaction alkaloids alkanes alkenation alkene complexes alkenes alkyl halides alkylation alkyne complexes alkynes allenes allylation allyl complexes aluminum amides amination amines amino acids amino alcohols amino aldehydes annulation annulenes antibiotics antifungal agents antisense agents antitumor agents antiviral agents arene complexes arenes arylation arynes asymmetric catalysis asymmetric synthesis atropisomerism autocatalysis azapeptides azasugars azides azo compounds barium benzylation betaines biaryls bicyclic compounds biomimetic synthesis bioorganic biosynthesis boron bromine calixarenes carbanions carbene complexes carbenes carbenoids carbocation carbocycles carbohydrates carbonyl complexes carbonylation carboxylic acids catalysis catenanes cations cavitands chelates chemoselectivity chiral auxiliaries chiral pool chiral resolution chirality chromium chromophores cleavage clusters combinatorial complexes condensation conjugation copper coupling cross-coupling crown compounds cryptands cuprates cyanines cyanohydrins cyclization cycloaddition cyclodextrines cyclopentadienes cyclophanes dehydrogenation dendrimers deoxygenation desulfurization diastereoselectivity diazo compounds diene complexes Diels-Alder reaction dihydroxylation dimerization diols dioxiranes DNA domino reaction drugs electrocyclic reactions electron transfer electrophilic addition electrophilic aromatic substitution elimination enantiomeric resolution enantioselectivity ene reaction enols enones enynes enzymes epoxidation epoxides esterification esters ethers fluorine free radicals fullerenes furans fused-ring systems gas-phase reaction genomics glycolipids glycopeptides glycosidases glycosides glycosylation green chemistry Grignard reaction halides halogenation halogens Heck reaction helical structures heterocycles heterogeneous catalysis Jain International Residential School Jakkasandra Post, Kanakapura Taluk Bangalore high-throughput JSS Public School, HSR Layout No 4/A, 14th Main, 6th Sector HSR Layout, Bangalore screening HIV homogeneous catalysis host-guest systems hydrazones hydrides hydroboration hydrocarbons hydroformylation hydrogen transfer hydrogenation Freedom International School C A # 33, Sector IV HSR Layout, Bangalore hydrolysis hydrosilylation hydrostannation hyperconjugation imides imines indium indoles induction inhibitors insertion iodine ionic liquids iridium iron isomerization The Brigade International School , Brigade Millenium JP Nagar Brigade Millenium, JP Nagar Bangalore ketones kinetic resolution lactams lactones lanthanides Lewis acids ligands lipids lithiation lithium macrocycles magnesium manganese Mannich bases medicinal chemistry metalation metallacycles metallocenes metathesis Michael addition Mitsunobu reaction molecular recognition molybdenum multicomponent reaction nanostructures natural products neighboring-group effects nickel nitriles nitrogen nucleobases nucleophiles nucleophilic addition nucleophilic National Centre For Excellence 154/1, “Victorian Enclave”, 5th Main, Malleshpalya, Bangalore aromatic substitution nucleosides nucleotides olefination oligomerization oligonucleotides oligosaccharides organometallic reagents osmium oxidation oxygen oxygenations ozonolysis palladacycles palladium peptides pericyclic reaction peroxides phase-transfer catalysis phenols pheromones phosphates phosphorus phosphorylation Adugodi Aga Abbas Ali Road Agaram Agrahara Dasara Halli Agrahara Dasarahalli Airport Exit Road Airport Main Road Airport Road Akkipet Ali Askar Road Alur Venkatarao Road Amarjyothi Layout Amruth Nagar Amrutha Halli Ananda Nagar Anandrao Circle Anche Palya Ane Palya Anekal Anjana Nagar Anubhava Nagar APMC Yard Arabic College Arakere Arcot Sreenivasachar Street Ashok Nagar Ashwath Nagar Attibele Attiguppe Austin Town Avala Halli Avenue Road B. Narayanapura Babusahib Palya Bagalagunte Bagalur Balaji Nagar Balepet Banashankari Banashankari 1st Stage Banashankari 2nd Stage Banashankari 3rd Stage Banaswadi Banaswadi Ring Road Bangalore G.P.O Bannerghatta Bannerghatta Road Bapuji Nagar Basappa Circle Basava Nagar Basavanagudi Basaveshwara Nagar Basaveshwara Nagar 2nd Stage Basaveshwara Nagar 3rd Block Basaveshwara Nagar 3rd Stage Basaveshwara Road Bazaar Street Begur BEL Road Bellandur Bellandur Outer Ring Road Bellary Road BEML Layout Benagana Halli Bendre Nagar Benson Town Bharati Nagar Bhattara Halli Bhoopasandra Bhuvaneshwari Nagar Bidadi Bileka Halli Bilekahalli Binny Mill Road Bismillah Nagar Bommana Halli Bommanahalli Kendriya Vidyalaya Malleswaram 18th Cross Malleswaram Bangalore Bommasandra Bommasandra Industrial Area Brigade Road Brindavan Nagar Brookefield Brunton Road BTM 1st Stage BTM 2nd Stage Bull Temple Road Palace Orchards/Sadashivnagar area located north city centre IITJEE SKMClasses.weebly.com property prices higher brackets possibly IITJEE SKMClasses.weebly.com up-market residential area in Bangalore M.G. Road/Brigade Road M.G. Road skmclasses.weebly.comBrigade Road main commercial areas Bangalore. Residential areas nearbyIITJEE SKMClasses.weebly.com Brunton Road Rest House Road, St. Mark’s Road skmclasses.weebly.comLavelle Road Airport Road/Indiranagar eastern suburb, Indiranagar is easily accessible IITJEE city centre skmclasses.weebly.com Airport Koramangala Located south Indiranagar, Koramangala quite favourite IITJEE SKMClasses.weebly.com IT professionals Despite 7 kmsIITJEE SKMClasses.weebly.com city centre, property values Ulsoor scenic man-made lake Ulsoor seen a spurt building activity last few years.IITJEE SKMClasses.weebly.com proximityIITJEE SKMClasses.weebly.com M.G Road jacked up property prices here Jayanagar/J.P. Nagar/Banashankari proximity areas Electronic City main reason skmclasses.weebly.comtheir growth recent past Jayanagar largest colonies Asia skmclasses.weebly.comthese areas popular areas Bangalore. Jayanagara originally namedIITJEE SKMClasses.weebly.com Sri Jayachamarajendra wodeyar last king Mysore. Later Sri Kumaran Children’s Home Survey No 44 – 50, Mallasandra Village Uttarahalli Hobli, Off Kanakapura Main Road, Bangalore skmclasseslocality namedIITJEE SKMClasses.weebly.com current DD kendra is situated known IITJEE skmclasses.weebly.com JC Nagar or Jayachamarajendra Nagar Delhi Public School, North Campus Survey No. 35/A, Sathanur Village Jala Hobli, Bangalore Jayanagar IITJEE SKMClasses.weebly.com literally Victory City Jayanagar IITJEE skmclasses.weebly.com traditionally regarded IITJEE skmclasses.weebly.com southern end Bangalore South End Circle “, wherein six roadsIITJEE SKMClasses.weebly.com different areas meet skmclasses.weebly.com historic Ashoka Pillar mark southern end city bear this fact. newer extensions IITJEE SKMClasses.weebly.com taken away this distinctionIITJEE SKMClasses.weebly.com Jayanagar still remains one IITJEE SKMClasses.weebly.com southern parts city Malleshwaram Basavanagudi Malleshwaram north Bangalore, Basavanagudi south IITJEE SKMClasses.weebly.com areas oldest Bangalore skmclasses.weebly.com residents IITJEE SKMClasses.weebly.com original inhabitants City. Malleswaram PSBB Learning Leadership Academy
# 52, Sahasra Deepika Road, Laxmipura Village, Off Bannerghatta Main Road Bangalore located actually north-west Bangalore derives IITJEE SKMClasses.weebly.com name IITJEE SKMClasses.weebly.com famous Kaadu Malleshwara temple 8th Cross in Malleshwaram, skmclasses.weebly.comGandhibazar/ DVG Road in Basavanagudi IITJEE SKMClasses.weebly.com popular areas in Bangalore skmclasses.weebly.comshopping during festival times. Malleswaram been homeIITJEE SKMClasses.weebly.com several important personalities skmclasses.weebly.cominstitutions. Bangalore’s own Nobel laureate, C.V. Raman, late Veena Doreswamy Iyengar skmclasses.weebly.com M.Chinnaswamy cricket stadium is named, academician M.P.L. Sastry, poet G.P. Rajaratnam skmclasses.weebly.com Dewan Seshadri Iyer institutions IITJEE SKMClasses.weebly.com Canara Union club Konkani-speaking people in 1930 IITJEE SKMClasses.weebly.comIITJEE SKMClasses.weebly.com this day hosts a variety cultural activities Malleswaram Association, hub area’s sporting activity since 1929 skmclasses.weebly.com Chowdaiah Memorial hosting great names music skmclasses.weebly.comtheatre. AccordingIITJEE SKMClasses.weebly.com recent figures available IITJEE SKMClasses.weebly.com Bangalore Development Authority BDA Malleswaram’s net population density is 521 personsIITJEE SKMClasses.weebly.com hectare, Bangalore City Corporation standard is 352IITJEE SKMClasses.weebly.com hectare Sadhashivnagar Sadashivanagar arguably IITJEE SKMClasses.weebly.com elite skmclasses.weebly.comexpensive neighborhood in Bangalore India fashionable among politicians, movie starsIITJEE SKMClasses.weebly.com millionaires afford homes “Beverly Hills Bangalore,” having IITJEE SKMClasses.weebly.com address in Sadashivanagar connotes high level prestige success fame Vijayanagar derivesIITJEE SKMClasses.weebly.com nameIITJEE SKMClasses.weebly.com Vijayanagara empire IITJEE SKMClasses.weebly.com flourished in south India during 15th skmclasses.weebly.com16th centuries.Vijayanag ar East is popularly known IITJEE base skmclasses.weebly.com RPC Layout (Railway Parallel Colony Layout), since this layout is along railway track. IITJEE skmclasses.weebly.com recently renamed Hampi Nagar Hampi capital Vijayanagar Empire Vijayanagar houses a large Public Library, IITJEE SKMClasses.weebly.com is one largest in Karnataka Halasuru Halasuru formerly known IITJEE skmclasses.weebly.com Ulsoor oldest neighbourhoods Indian city Bangalore predominant Tamil speaking population renowned skmclasses.weebly.com numerous temples skmclasses.weebly.comrather narrow streets skmclassesprominant areas CityIITJEE SKMClasses.weebly.com Sanjay Nagar skmclasses.weebly.com RT Nagar, Hebbal, Vyalikaval, Yeshwanthpur, Sriramapura, Rajajinagar, Rajarajeshwarinagar, Chickpet, Chamarajpet, V V Puram, Mavalli, Hanumanthanagar, Padmanabhanagar Hosakerehalli Sarakki, BTM Layout, Domlur, Gandhinagar, Vasanthanagar, Vivek Nagar, Cox Town, Frazer Town Benson Town Bangalore Roads Many roads Bangalore had European names South Parade Road, Albert Victor Road, Hardinge Road, Grant Road several roads Bangalore derived Delhi Public School Sarjapur, Bangalore East Survey No.43/1B & 45, Sulikunte Village, Dommasandra Post, Bangalore IITJEE SKMClasses.weebly.com military nomenclature Mahatma Gandhi Road MG Raod called IITJEE skmclasses.weebly.com South Parade Roadskmclasses.weebly.com nomenclature Independence Edify School Electronic City
105, 34th Main, 23rd Cross, Sector-A, Surya Nagar Phase-2, Anekal-Chandapura Main Road, Electronic City Chamarajpet First Main Road named Albert Victor Road 1889 future King Edward VII Englskmclasses.weebly.com renamed Alur Venkatarao Road,IITJEE SKMClasses.weebly.com well-known Kannada writer skmclasses.weebly.comprotagonist unification National Public School, Koramangala National Games Village Koramangala, Bangalore Kannada-speaking areas andlater shortened IITJEE skmclasses.weebly.com A.V. Road. Avenue road earlier known Doddapete Infantry Road became Bhagavan Mahaveer Road 2004 Chamarajendra Park Jyothi Kendriya Vidyalaya Yelachenahalli, Kanakapura Road Bangalore IITJEE skmclasses.weebly.com Cubbon Park IITJEE SKMClasses.weebly.com Sir Mark Cubbon British Commissioner Mysore mid-19th century. Fraser Town, IITJEE SKMClasses.weebly.com named Sir Stuart Fraser scholar tutor Maharaja Krishnaraja Wadiyar IV Pulakeshinagar. Hardinge Road old name Pampa Mahakavi Road. sometime, Cunningham Road crowded bazaar being called Sampangi Ramaswamy Temple Road Race Course Road became Devraj Urs Road National Public School, Rajajinagar 1036-A, Purandarapura, V Block, Rajajinagar, Bangalore skmclasses.weebly.comGrant Road became Vittal Mallya Road IITJEE SKMClasses.weebly.com two Vittal Mallya Roads skmclasses bund Sampangi Tank Kanteerava Stadium Gear Innovative International School GEAR Road, Doddakannelli, Off Sarjapur Road & Outer Ring Road, Bangalore IITJEE SKMClasses.weebly.com built MacIver Town Shantala Nagar Assayee Road Meanee Road those names commemoration wars fought Madras New Horizon Gurukul Ring Road Marathalli, Behind New Horizon College of Engineering, Bangalore , Bangalore IITJEE skmclasses.weebly.com Sappers, BGS National Public School Ramalingeshwara Cave Temple Hulimavu, Bangalore IITJEE SKMClasses.weebly.com Presidency School (Bangalore – East) CA Site 7P1A, 2nd A Main, 3rd A cross, East of NGEF Layout, Kasturinagar, Bangalore British Army against Marathas first decade 19th century Basavanagudi, meaning temple Basava skmclasses.weebly.com big bull situated area reason behind naming area Basavanagudi extension skmclassesformed around 1900. Gandhi Bazar, earlier known merely Angadi Beedhi School Of India Anekal Road, Bannerghatta, Bangalore skmclasses formed Kumarapark came skmclasses existence 1947, year Indian Independence, whereas Jayanagar skmclasses.weebly.comRajajinagarIITJEE SKMClasses.weebly.com thought year later 1948 skmclasses.weebly.com orchards Bangalore Palace skmclasses developed housing colony skmclasses.weebly.comnamed Sadashivanagar 1960,IITJEE SKMClasses.weebly.com Orchids The International School Jalahalli, Nagarbavi, Mysore Road, Sarjapur Road, BTM, Bangalore well-known freedom fighter Dakshina Kannada Karnad Sadashiva Rao BVK Iyengar Road Byappana Halli Byatarayanapura Byrasandra C.V Raman Nagar Cambridge Layout Cambridge Road Cantonment Carmelaram Castle Street Central Street Chamarajapet Shanthi Theatre South End Circle INOX Shree Garuda Swagath Mall, 4th Floor, Tilak Nagar Main Road INOX Bangalore Central-2, 5th Floor, 45th Cross Maheshwari Theater Bannerghatta Main Road Gopalan Cinemas Gopalan Innovation Mall, JP Nagar 3rd Phase Chandapura Chandra Layout Global Academy For Learning Sri Chowdeshwari Farm, Near Global Village IT Park, National Public School, HSR Layout P2/32, Sector 4, HSR Layout Bangalore Pattanagere Main Road, Rajarajeshwarinagar, Bangalore Chickpet Chikkabanavara Chikkadugodi Chikkallasandra Chikkamavalli Cholara Palya Chowdeshwari Temple Street Chunchagatta Church Street Clevelskmclasses.weebly.com Town CMH Road Coles Park Commercial Street Commissariat Road Cooke Town Corporation Circle Cottonpet Cox Town Crescent Road Cubbon Park Cubbon Road Cubbonpet Cunningham Road Dairy Circle Dasara Halli Dasarahalli Devaiah Park Devana Halli Devanahalli Devara Chikkana Halli Devara Jeevana Halli Devasandra Dharmaram College Dickenson Road Dispensary Road Dodda Banaswadi Dodda Bommasandra Dodda Kallasandra Dodda Kanna Hally Dodda Mavalli Doddaballapur Road Doddaballapura Doddana Kundi Dollars Colony Domlur Domlur 2nd Stage Domlur Ring Road Dooravani Nagar Dr. Ambedkar Veedhi Dr. DVG Road Delhi Public School, South 11 K.M., kanakapura Road Konanakunte Post, Bangalore Dr. Raj Kumar Road Dr. TCM Royan Road Ejipura Electronic City Field Marshal Cariappa Road Frazer Town Ganapathi Nagar Gandhi Bazaar Gandhi Nagar Ganga Nagar Gangadhar Chetty Road Ganigarpet Garvebhavi Palya Gavipuram Extension Gayathri Nagar Geddala Halli Geddalahalli Giri Nagar Giri Nagar 1st Phase Giri Nagar 2nd Phase GM Palya Gokula Golf Course Road Gorgunte Palya Govindaraj Nagar Green Park Extension, Guddada Halli Gundopanth Street National Public School, Indiranagar 12 A Main HAL II Stage, Bangalore H.Siddaiah Road Haines Road HAL HAL 2nd Stage HAL 3rd Stage HAL Airport Road Hampi Nagar Hanumantha Nagar Hayes Road HBR Layout Hebbal Kempapura Hebbal Ring Road Hegde Nagar Heggana Halli Hennur Hesaraghatta HKP Road HMT Layout Hongasandra Hoody Horamavu Hosakere Halli photochemistry photooxidation piperidines polyanions polycations polycycles polymers Porphyrins prostaglandins protecting groups Entrance Coaching IIT Entrance Coaching CLAT Entrance Coaching AICEE Coaching TANCET Entrance Coaching PMT Entrance Coaching Language Classes Spoken English Classes Spoken Hindi Classes Foreign Languages Coaching Spoken Kannada Classes Spoken Gujarati Classes Competitive Exams Coaching KMAT Coaching Online CAT Coaching GATE Coaching IBPS Coaching RRB Coaching Civil Services Coaching UGC Net Coaching SSB & NDA Coaching UPSC Coaching IAS Coaching TNPSC Coaching Accounts & Finance CA Training PHP & MySQL Training Spring Training Web Designing Training Administration Training VMWare Training ITIL Training SharePoint Training SAN Training Linux Administration Training Database Training Data Warehousing Training Database Testing Training HADOOP Training Oracle DBA Training SQL Server Training Programming Languages Java & J2EE Training C C++ Training Perl Programming Training Python Programming Training Shell Scripting Training Mobile Development Training Android Development Training iPhone Development Training Mobile Application Testing Training Mobile Gaming Training Mobile Application Development Training Oakridge International School Oakridge International School, Sarjapur Road, , Bangalore School of India, Bannerghatta, Bangalore Delhi Public School DPS North Campus, Yelahanka, Bangalore Jain International Residential School (JIRS), Jakkasandra Post, Bangalore Delhi Public School (DPS East), Sarjapur, Bangalore TREAMIS World School, Electronics City, Bangalore South Delhi Public School (South), Kanakapura Road, Bangalore The Deen’s Academy, Whitefield, Bangalore National Public School (NPS), Koramangala, Bangalore Royale Concorde International School, Kalyan Nagar, Bangalore Freedom International School, HSR Layout, Bangalore Air Force School Army Public School Bangalore Military School BGS International School Cambridge Public School Delhi Public School Deva Matha Central School Jain International Residential School Kendriya Vidyalaya A M C School A.S.C Public School Amara Jyothi Public School Anand Shiksha Kendra ICSE Syllabus ACTS Secondary School B Mona High School Baldwin Boys High School Baldwin Girls High School Bishop Cotton Boys School Bishop Cotton Girls School Brigade School Candor International School Cambridge Public School Cathedral High School Chinmaya Vidyalay Christ Academy Ekya School Gnan Srishti School of Excellence Gopalan National School India International School IIS Lawrence School-ICSE New Horizon Public School Notre Dame Academy Paradise Residential School Patel Public School Podar International School Prakriya Green Wisdom School Primus School Ryan International School Sishu Griha St. Francis De Sales (SFS) High School Sherwood High Sri Kumaran Childrens Home St Francis School St Johns High School St Thomas Public School St. Patricks Academy St. Peters School Vibgyor High CBSE Syllabus AECS Magnolia Maaruti Public School Amaatra Academy Amrita Vidyalayam BGS-NPS School Brigade School BRS Global Centre for Excellence Capitol Public School CMR National Public School Delhi Public School East, South, North Edify School EuroSchool Freedom International School Geethanjali Montessori Geethanjali Vidhyalaya Gitanjali International School GISB Greengrove International School Gomathy Global School Harvest International School JSS Public School Kendriya Vidyalaya KV Manipal Tattva School Mirambika School for New Age NITTE International School National Centre for Excellence NCFE National Public School New Horizon Gurukul NHG Oakridge International School Presidency School PSBB LLA Padma Seshadri Bal Bhavan Radcliffe School Ravindra Bharathi Global School Sadhguru Sainath International School SSI Sri Kumaran Childrens Home Sunrise International Residential School Sujaya School The Samhita Academy Vagdevi Vilas School Venkat International Public School VIPS Vyasa International School Zee School IGCSE Syllabus Asia Pacific World School Krupanidhi Cambridge International School Candor International School Ekya School Gitanjali International GISB Greengrove International School Gomathy Global School Gopalan International School Harvest International School India International School (IIS) Oakridge International School Primus School Shibumi Trio World School International Baccalaureate IB Candor International School Oakridge International School (IB-PYP) State Board Amaatra Academy Lawrence School-State Board Paradise Residential School Primus School St. Francis De Sales (SFS) High School Sri Kumaran Childrens Home St Francis School Vagdevi Vilas School Special Schools Sri Rakum School for the blind Mirambika School for New Age Sri Aurobindo Shibumi (J. Krishnamurthi Aurinko Academy Chetana Kini Institute Samarthanam Residential School XSeed Schools Mirambika School New Age Sri Aurobindo Mother Teresa Public School curriculum Chrysalis High List of Schools Achievers International Academy ACTS Secondary School Amaatra Academy Amar Jyothi School Amrita Vidyalayam Army Public School Asia Pacific World School Aurinko Academy B Mona High School Baldwin Boys High School Baldwin Girls High School Bangalore International School Bangalore School Bethany High Bethany Junior School BGS-NPS School Bishop Cotton Boys School Bishop Cotton Girls School Brigade School British International School BRS Global Centre for Excellence BVM Global Cambridge Public School Candor International School Capitol Public School Cathedral High School Chinmaya Vidyalaya Christ Academy Chrysalis High CMR National Public School Delhi Public School Deva Matha Central School Edify School Ekya School EuroSchool Freedom International School Gear School Geethanjali Montessori Geethanjali Vidhyalaya Gitanjali International (GISB) Global Indian International School Gnan Srishti School Gomathy Global School Gopalan School Green County Public School Greengrove International School Greenwood High Harvest International School India International School Innisfree House School JSS Public School Kendriya Vidyalaya (KV) Lawrence School ICSE Lawrence School-State Magnolia Maaruti Public School Manipal Tattva School Mirambika School for New Age Mother Teresa Public School National Centre for Excellence National Hill View Public School National Public School New Horizon Gurukul New Horizon Public School Nitte International School Notre Dame Academy Oakridge International School Oxford Public School Parachute Regiment School Paradise Residential School Patel Public School Podar International School Prakriya Green Wisdom School Presidency School Primus School PSBB LLA Radcliffe School Ravindra Bharathi Global School Ryan International School Sadhguru Sainath International School Samarthanam Residential School SFS High School Sherwood High Shibumi Silver Oaks Sishu Griha Sri Chaitanya Techno School Sri Kumaran Childrens Home Sri Rakum School for the blind St Francis School St Johns High School St Mira School St Thomas Public School St. Patrick’s Academy St. Peters School Sujaya School Sunrise International Residential School The Samhita Academy Trio World School Vagdevi Vilas School Venkat International Public School Vibgyor High Vidyaniketan School Vyasa International School Whitefield Global School Xseed Pre-School Zee School
Primary Years Programme Colegio Anglo Mexicano MEXICO Milgate Primary School, AUSTRALIA Diploma Programme Australian International School Indonesia Pejaten Campus INDONESIA Instituto Educativa Fiscomisional Celina Vivar Espinosa, ECUADOR Unidad Educativa Juan de Salinas, ECUADOR Primary Years Programme Academia Moderna Charter, UNITED STATES Beacon School BRAZIL Dr. Orlando Edreira Academy, School 26, UNITED STATES Westhill Institute Carpatos Elementary Campus, MEXICO Westhill Institute, S.C. MEXICO Middle Years Programme Cooper Academy, UNITED STATES European International School VIETNAM Mark Bills Middle School UNITED STATES Mount Washington School UNITED STATES UCSI International School MALAYSIA Diploma Programme Cass Technical High School, UNITED STATES Colegio Experimental Juan Montalvo, ECUADOR Colegio Miguel Moreno Ordoñez de Cuenca ECUADOR Colegio Nacional Ibarra ECUADOR Colegio Nacional Mariano Benítez ECUADOR Colegio Nacional Velasco Ibarra, ECUADOR Colegio Nacional Veracruz, ECUADOR Colegio Pedro Vicente Maldonado ECUADOR Colegio Técnico 12 de Febrero, ECUADOR Colegio Técnico Fiscomisional Ecuador Amazónico, ECUADOR Colegio de Bachillerato Limón ECUADOR King Fahd Academy Bonn GERMANY Saudi Schools Moscow RUSSIAN FEDERATION Unidad Educativa 17 de Julio ECUADOR Unidad Educativa 12 de Febrero ECUADOR Unidad Educativa Bernardo Valdivieso ECUADOR Unidad Educativa Dayuma ECUADOR Unidad Educativa Federico González Suárez ECUADOR Unidad Educativa Fiscomisional Fray Bartolomé de las Casas ECUADOR Unidad Educativa Fiscomisional Juan Pablo II ECUADOR Unidad Educativa Fiscomisional San José de Calasanz ECUADOR Unidad Educativa León Ruales ECUADOR Unidad Educativa Nacional Napo ECUADOR Unidad Educativa Temporal Camilo Gallegos Dominguez ECUADOR Unidad Educativa Temporal Manuel Córdova Galarza ECUADOR Primary Years Programme Campus International School, UNITED STATES Carl Hankey K-8 School UNITED STATES Christa McAuliffe Elementary School UNITED STATES Goethe International Charter School , UNITED STATES Hammond Eastside Elementary Magnet School, UNITED STATES Hawthorne Elementary School UNITED STATES Idlewild Elementary School, UNITED STATES J. Colin English Elementary UNITED STATES Jose de Escandon Elementary, UNITED STATES Lincoln Elementary School, UNITED STATES Qingdao Amerasia International School CHINA Roland Park K-8 Magnet School for International Studies, UNITED STATES Theodore Roosevelt Elementary School, UNITED STATES Woodrow Wilson Elementary UNITED STATES Middle Years Programme Cache La Poudre Middle School, UNITED STATES Carl Hankey K-8 School, UNITED STATES Cedar Shoals High School UNITED STATES Concord High School, UNITED STATES Harry Stone Montessori Academy, UNITED STATES International School of Monterey, UNITED STATES Johnnie R. Carr Middle School, UNITED STATES Prairie Seeds Academy, UNITED STATES Roland Park K-8 Magnet School, UNITED STATES Sterling Middle School UNITED STATES The Aga Khan Academy, Hyderabad, INDIA Diploma Programme Ausangate Bilingual School PERU Author’s School Istochnik RUSSIAN FEDERATION Colegio Fiscal Técnico El Chaco ECUADOR Colegio Juan Bautista Montini ECUADOR Colegio Nacional Ciudad de Cuenca ECUADOR Colegio Nacional Experimental Salcedo, ECUADOR Colegio Nacional Machachi, ECUADOR Colegio Nacional Mixto El Playon, ECUADOR Colegio Técnico Cascales, ECUADOR Dar al Marefa Private School, UNITED ARAB EMIRATES Escola Internacional del Camp SPAIN Gymnasium Jovan Jovanovic Zmaj SERBIA ISTEK Private Acibadem Schools TURKEY Instituto Superior Tecnológico Carlos Cisneros ECUADOR Instituto Superior Tecnológico Daniel Alvarez Burneo ECUADOR Instituto Técnico Superior Isabel de Godin ECUADOR King Abdulaziz Saudi School Rome ITALY Riga State Gymnasium Nr. 2 LATVIA Saudi School Vienna AUSTRIA State IS Seeheim Jugenheim/Schuldorf Bergstrasse GERMANY Unidad Educativa Bolívar, ECUADOR Unidad Educativa Abelardo Moncayo, ECUADOR Unidad Educativa Fiscomisional Verbo Divino, ECUADOR Unidad Educativa Mayor ECUADOR Unidad Educativa Nueva Semilla, ECUADOR Unidad Educativa Temporal Juan Bautista Vásquez, ECUADOR Primary Years Programme Ajman Academy UNITED ARAB EMIRATES British International School Kiev UKRAINE Cache La Poudre Elementary School, UNITED STATES Dr. Thomas S. O Connell Elementary School UNITED STATES Gems World Academy Abu Dhabi UNITED ARAB EMIRATES Hebron-Harman Elementary School, UNITED STATES International School of Solothurn, SWITZERLAND Lisa-Junior Primary School AUSTRIA Madison Richard Simis Elementary School, UNITED STATES Miina Härma Gümnaasium, ESTONIA Riffenburgh Elementary School UNITED STATES Roscoe Wilson Elementary School, UNITED STATES Singapore International School INDIA William H. Wharton K-8 Dual Language Academy UNITED STATES World Academy of Tirana, ALBANIA École Centrale, CANADA École Micheline-Brodeur CANADA École Saint-Édouard, CANADA École élémentaire catholique Jean-Paul II CANADA Özel Istanbul Coskun Koleji Anaokulu & Ilkokulu TURKEY Middle Years Programme Abraham Lincoln Middle School UNITED STATES Beijing Huijia Private School CHINA Cakir Middle School TURKEY Durango High School UNITED STATES Emirates IS Meadows, UNITED ARAB EMIRATES Madison International School, MEXICO Meadow Park Middle School, UNITED STATES North Central High School, UNITED STATES Phuket International Academy Day School THAILAND Ray Wiltsey Middle School UNITED STATES Rockridge Secondary School CANADA School Lane Charter School UNITED STATES Strothoff International School Rhein-Main Campus Dreieich GERMANY Tsukuba International School JAPAN École Père-Marquette, CANADA École secondaire Saint-Luc, CANADA Diploma Programme Anania Shirakatsy Armenian National Lyceum Ed’l Complex-CJSC, ARMENIA COLEGIO ALAUDA SPAIN Colegio Británico, MEXICO Colegio Nacional Camilo Gallegos Toledo ECUADOR Colegio Nacional Experimental Amazonas, ECUADOR Colegio Nacional Experimental María Angélica Idrobo, ECUADOR Colegio Nacional San José, ECUADOR Eastern Mediterranean International School, ISRAEL Emirates National School UNITED ARAB EMIRATES GEMS American Academy Abu Dhabi, UNITED ARAB EMIRATES German International School Sharjah UNITED ARAB EMIRATES Instituto Tecnológico Superior Angel Polibio Chaves, ECUADOR International School Moshi Arusha Campus TANZANIA, UNITED REPUBLIC OF International School of Bydgoszcz POLAND Ludoteca Elementary & High School, Padre Víctor Grados, ECUADOR Léman International School Chengdu CHINA Metropolitan School of Panama, PANAMA Munic. Atms. Educ. Institution Kogalym Secondary School ?8, RUSSIAN FEDERATION Phorms Bilingual Gymnasium, GERMANY Royal High School, UNITED STATES SIS Swiss International School Stuttgart-Fellbach, GERMANY Seedling Public School INDIA The British School of Beijing CHINA Unidad Educativa Fiscal Experimental del Milenio, ECUADOR Unidad Educativa Juan de Velasco ECUADOR Unidad Educativa Tumbaco, ECUADOR École secondaire Gaétan Gervais, CANADA École secondaire Hanmer CANADA Stonehill International School American School of Bombay Mumbai Day school offering PYP MYP DP Dhirubhai Ambani International School Mumbai Day school offering DP Ecole Mondiale World School, Mumbai Day school offering DP Jamnabai Narsee School Mumbai Day school offering DP Ahmedabad International School Ahmedabad Day School offering PYP Mahatma Gandhi International School Ahmedabad Day school offering MYP Mahindra United World College of India Pune Boarding school offering DP Mercedes-Benz International School Pune American Embassy School Delhi Day school offering DP The British School, Delhi Day school offering DP Pathways World School, Gurgaon Boarding school offering PYP DP SelaQui World School, Dehra Dun Boarding school offering DP Canadian International School, Bangalore Mixed Boarding Day school offering DP International School of Bangalore, Bangalore Mixed Boarding Day school offering DP Oakridge International School Hyderabad Day school offering PYP Chinmaya International Residential School Coimbatore Boarding school offering DP Good Shepherd International School Ooty Boarding school offering DP Kodaikanal International School, Kodaikanal Boarding school offering DP Home Tuition Group teachers available small groupsstudents IB International Baccalaureate Programme, IGCSE, ISc, ICSE, CBSE Schools offering IB ( International Baccalaureate ) Programme Bangalore International School Geddalahalli Hennur Bagalur Road Kothanur Post Bengaluru India 560 077 Stonehill International School, 1st Floor, Embassy Point #150, Infantry Road Bengaluru 560 001 Stonehill International School 259/333/334/335 Tarahunise Post Jala Hobli, Bengaluru North 562157 Candor International School Begur Koppa Road, Hullahalli Off Bannerghatta Road, Near Electronic City Bangalore 560105 Greenwood High International School Bengaluru, No.8-14, Chickkawadayarapura, Near Heggondahalli Gunjur Post, Varthur Sarjapur Road, Bangalore 560087 Sarla Birla Academy, Bannerghatta, Bangalore, Canadian International School, Yelahanka, Bangalore Indus International School Billapura Cross Sarjapur Bangalore
Krishnappa Layout
Tuition at Krishnappa Layout
Tution at Krishnappa Layout
Krishnappa Layout tution
Chaithanya Layout
Tuition at Chaithanya Layout
Tution at Chaithanya Layout
Chaithanya Layout tution
Thimma Reddy Layout
Tuition at Thimma Reddy Layout
Tution at Thimma Reddy Layout
Thimma Reddy Layout tution
Chandrareddy Layout
Tuition at Chandrareddy Layout
Tution at Chandrareddy Layout
Chandrareddy Layout tution
Addischetan Layout
Tuition at Addischetan Layout
Tution at Addischetan Layout
Addischetan Layout tution
Chamundeshwari Layout
Tuition at Chamundeshwari Layout
Tution at Chamundeshwari Layout
Chamundeshwari Layout tution
Omkar Nagar Layout
Tuition at Omkar Nagar Layout
Tution at Omkar Nagar Layout
Omkar Nagar Layout tution
Mico Layout
Tuition at Mico Layout
Tution at Mico Layout
Mico Layout tution
Lakshmi Layout
Tuition at Lakshmi Layout
Tution at Lakshmi Layout
Lakshmi Layout tution
Sun City Layout
Tuition at Sun City Layout
Tution at Sun City Layout
Sun City Layout tution
Nataraja Layout
Tuition at Nataraja Layout
Tution at Nataraja Layout
Nataraja Layout tution
Santrupthi Nagar
Tuition at Santrupthi Nagar
Tution at Santrupthi Nagar
Santrupthi Nagar tution
Silver Oak Layout
Tuition at Silver Oak Layout
Tution at Silver Oak Layout
Silver Oak Layout tution
Balaji Layout
Tuition at Balaji Layout
Tution at Balaji Layout
Balaji Layout tution
Royal Meridian Layout
Tuition at Royal Meridian Layout
Tution at Royal Meridian Layout
Royal Meridian Layout tution
Vakil Marina Layout
Tuition at Vakil Marina Layout
Tution at Vakil Marina Layout
Vakil Marina Layout tution
Vakil Garden City
Tuition at Vakil Garden City
Tution at Vakil Garden City
Vakil Garden City tution
Lake City
Tuition at Lake City
Tution at Lake City
Lake City tution
Ranka Colony
Tuition at Ranka Colony
Tution at Ranka Colony
Ranka Colony tution
Virat Nagar
Tuition at Virat Nagar
Tution at Virat Nagar
Virat Nagar tution
Sundarram Shetty Nagar
Tuition at Sundarram Shetty Nagar
Tution at Sundarram Shetty Nagar
Sundarram Shetty Nagar tution
BTS Layout
Tuition at BTS Layout
Tution at BTS Layout
BTS Layout tution
Patel Layout
Tuition at Patel Layout
Tution at Patel Layout
Patel Layout tution
Garvebhavi Palya
Tuition at Garvebhavi Palya
Tution at Garvebhavi Palya
Garvebhavi Palya tution
Papanna Reddy Layout
Tuition at Papanna Reddy Layout
Tution at Papanna Reddy Layout
Papanna Reddy Layout tution
Muni Reddy Layout
Tuition at Muni Reddy Layout
Tution at Muni Reddy Layout
Muni Reddy Layout tution
Muniyappa Layout
Tuition at Muniyappa Layout
Tution at Muniyappa Layout
Muniyappa Layout tution
Hanuman Nagar
Tuition at Hanuman Nagar
Tution at Hanuman Nagar
Hanuman Nagar tution
Anugraha Layout
Tuition at Anugraha Layout
Tution at Anugraha Layout
Anugraha Layout tution
Sarvabhauma Nagar
Tuition at Sarvabhauma Nagar
Tution at Sarvabhauma Nagar
Sarvabhauma Nagar tution
Panduranga Nagar
Tuition at Panduranga Nagar
Tution at Panduranga Nagar
Panduranga Nagar tution
Seenappa Layout
Tuition at Seenappa Layout
Tution at Seenappa Layout
Seenappa Layout tution
Nagarjun Enclave
Tuition at Nagarjun Enclave
Tution at Nagarjun Enclave
Nagarjun Enclave tution
Ramakrishna Nagar
Tuition at Ramakrishna Nagar
Tution at Ramakrishna Nagar
Ramakrishna Nagar tution
Kashi Nagar
Tuition at Kashi Nagar
Tution at Kashi Nagar
Kashi nagar tution
Naidu Layout
Tuition at Naidu Layout
Tution at Naidu Layout
Naidu Layout tution
Yelachenahalli
Tuition at Yelachenahalli
Tution at Yelachenahalli
Yelachenahalli tution
Doddakallasandra
Tuition at Doddakallasandra
Tution at Doddakallasandra
Doddakallasandra tution
Harsha Layout
Tuition at Harsha Layout
Tution at Harsha Layout
Harsha Layout tution
Kanka Nagar
Tuition at Kanka Nagar
Tution at Kanka Nagar
Kanka Nagar tution
Ilyas Nagar
Tuition at Ilyas Nagar
Tution at Ilyas Nagar
Ilyas Nagar tution
MG Layout
Tuition at MG Layout
Tution at MG Layout
MG Layout tution
Manjunath Garden
Tuition at Manjunath Garden
Tution at Manjunath Garden
Manjunath Garden tution
Elita Promenade
Tuition at Elita Promenade
Tution at Elita Promenade
Elita Promenade tution
Mysore Bank Colony
Tuition at Mysore Bank Colony
Tution at Mysore Bank Colony
Mysore Bank Colony tution
Jeewan Griha Colony
Tuition at Jeewan Griha Colony
Tution at Jeewan Griha Colony
Jeewan Griha Colony tution
Ayodya Nagar
Tuition at Ayodya Nagar
Tution at Ayodya Nagar
Ayodya Nagar tution
Ashta Laxmi Layout
Tuition at Ashta Laxmi Layout
Tution at Ashta Laxmi Layout
Ashta Laxmi Layout tution
Bank of Baroda Colony
Tuition at Bank of Baroda Colony
Tution at Bank of Baroda Colony
Bank of Baroda Colony tution
Mango Garden Layout
Tuition at Mango Garden Layout
Tution at Mango Garden Layout
Mango Garden Layout tution
Kailash Nagar
Tuition at Kailash Nagar
Tution at Kailash Nagar
Kailash Nagar tution
Vasantha Vallabha Nagar
Tuition at Vasantha Vallabha Nagar
Tution at Vasantha Vallabha Nagar
Vasantha Vallabha Nagar tution
Gubbalala
Tuition at Gubbalala
Tution at Gubbalala
Gubbalala tution
Anjanapura
Tuition at Anjanapura
Tution at Anjanapura
Anjanapura tution
Deepika Layout
Tuition at Deepika Layout
Tution at Deepika Layout
Deepika Layout tution
Jayanagar Housing Society Layout
Tuition at Jayanagar Housing Society Layout
Tution at Jayanagar Housing Society Layout
Jayanagar Housing Society Layout tution
Lingadheeranahalli
Tuition at Lingadheeranahalli
Tution at Lingadheeranahalli
Lingadheeranahalli tution
Raghuvanahalli
Tuition at Raghuvanahalli
Tution at Raghuvanahalli
Raghuvanahalli tution
Vajarahalli
Tuition at Vajarahalli
Tution at Vajarahalli
Vajarahalli tution
Thippasandra
Tuition at Thippasandra
Tution at Thippasandra
Thippasandra tution
Narayana Nagar
Tuition at Narayana Nagar
Tution at Narayana Nagar
Narayana Nagar tution
Vaikunta Hill
Tuition at Vaikunta Hill
Tution at Vaikunta Hill
Vaikunta Hill tution
Avalahalli
Tuition at Avalahalli
Tution at Avalahalli
Avalahalli tution
M K S Layout
Tuition at M K S Layout
Tution at M K S Layout
M K S Layout tution
MKS Layout
Tuition at MKS Layout
Tution at MKS Layout
MKS Layout tution
Ayappa Nagar
Tuition at Ayappa Nagar
Tution at Ayappa Nagar
Ayappa Nagar tution
Konanakunte
Tuition at Konanakunte
Tution at Konanakunte
Konanakunte tution
PNB Layout
Tuition at PNB Layout
Tution at PNB Layout
PNB Layout tution
Aditya Nagar
Tuition at Aditya Nagar
Tution at Aditya Nagar
Aditya Nagar tution
Sri Krishna Nagar
Tuition at Sri Krishna Nagar
Tution at Sri Krishna Nagar
Sri Krishna Nagar tution
Coconut Garden
Tuition at Coconut Garden
Tution at Coconut Garden
Coconut Garden tution
Bank Colony
Tuition at Bank Colony
Tution at Bank Colony
Bank Colony tution
Ganapathipura
Tuition at Ganapathipura
Tution at Ganapathipura
Ganapathipura tution
Kothnur Dinne
Tuition at Kothnur Dinne
Tution at Kothnur Dinne
Kothnur Dinne tution
small groups
small group of students
Geddalahalli
Hennur
Bagalur Road
Kothanur Post
tough words
Parl
Opal
Shopper Stop
Kasavanahalli
Differentiation
Calculus
IIT JEE Problems
Numarical
Integration
Algebra
Tuition lectures Material
Magnetic
Conductivity
Entropy
Kinetic Theory Gases
Cp Cv
Isothermal
Adiabatic
Isochoric
Isobaric Processes
Root Mean Square
Thermodynamics
Gravitation
Differential Equation
field
Potential
Mechanics
SHM
Projectile
series
Parallel
Learn Physics
Leran Mathematics
IPhO
APhO
IMO
Projectile
Latent Heat
Thermodynamics
Surface Tension
Viscosity
Accelerating Frame
velocity
wedge
mass
pulley
Moment Inertia
Roorkey Joint Entrance Exam
CET
Irodov
HC Verma
H C Verma
HCV Solutions
HC Verma Solutions
H C Verma Solutions
HCV Verma
Intermediate Algebra
Trigonometry
study material
preparation
Friction
sin
Modelling
cos
tan
cot
Gravitation
Electrostatics
sec
Field
cosec
Ellipse
Parabola
Hyperbola
inverse
string
Isochoric
Isobaric
Processes
Bending Stress
Strain
Geostationary Satellite
Entropy
Coefficient
Linear Expansion
Alpha Beta Gamma
Pendulum
Conductivity
Latent Heat
ice
water
Hydrometer
Glass
tube
travelling standing wave
Sound
Radiation
stefan Boltzmann law
Newton cooling
cylinder
Harmonic
Overtone
Resonance
Sonometer
Kunds
Beat
Frequency
vibration
tuning Fork
Swimmer
Young Bulk Modulus
welded chamber
MIT
Caltech
Yale
pipe
Magnetic
Tesla
Lenz
LvB
Buoyant
Buoyancy
Rho
efflux
Bernoullis
rare
Poiseuilles
Torricellis
critical
Terminal
Reynolds
Poise
coalescing
Laplace
Ventury
Hoop
orifice
Siphon
Foucault
stretched
compression
ball
scale
constant
length
shear
poisson Ratio
clock
loosing time
tvanausdal
vkiledj
Density
Partial Pressure
Humidity
Leak
SmartlearnwebTV
Space
Puncture
Photon
RC
RLC
LR Circuit
Electrical
Capacitor
Inductance
Linked
Flux
Wheatstone Bridge
Freelanceteach
Troutons Rule
Van Arkel Method
Overview
Metallurgy
Roasting
Calcination
Froth Floatation
Purification
Projected Area
PET Kerala
MPPET
Delta Star conversion
Internal Resistance
Battery
Trick Questions
Infinite Ladder
Quadratic
Cubic
Quartic
Quintic
NSEP
ckt
eqn
mesh
Folding
Lenzs
RMS
instantaneous
BCECE
MHCET
RPET
stepup
stepdown
transformer
Bilekahalli
UPSEAT
shunt
galvanometer
susceptibility
oscillating
magnetometer
pole strength
WB
west Bengal
Vacuum
Diode
Triode
Rectifier
Truth Table
Thermionic emission
Radioactivity
Half Life
Langmiur Child Law
FCC
BCC
Cube
Optics
Lens
Mirror
Focus
Focal
Concave
Convex
Lux
Phot
Lumen
Double slit
Complex
Integral
coordinate Geometry
compounds
Biochemistry
Some content on this page was disabled on October 5, 2016 as a result of a DMCA takedown notice from Reed Elsevier. You can learn more about the DMCA here:
https://wordpress.com/support/copyright-and-the-dmca/
Some content on this page was disabled on July 19, 2017 as a result of a DMCA takedown notice from Pearson Education, Inc.. You can learn more about the DMCA here: